An Alternative Formulation for the Five Point
Relative Pose Problem
People:
Dhruv Batra, Bart Nabbe, Martial HebertKeywords:
Epipolar matrix estimation, minimal correspondences, Quadratically constrained quadratic programming (QCQP)
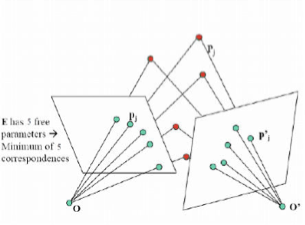
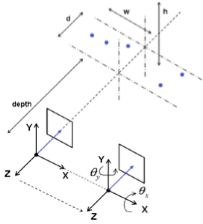
Figure
1: (Left) Two camera setup with minimal case of five
point correspondences; (Right) Geometry of the setup
used to create test data.
Abstract
The “Five Point Relative Pose Problem” is to find all possible camera configurations between two calibrated views of a scene given five point-correspondences. We take a fresh look at this well-studied problem with an emphasis on the parametrization of Essential Matrices used by various methods over the years. Using one of these parametrizations, a novel algorithm is proposed, in which the solution to the problem is encoded in a system of nine quadratic equations in six variables, and is reached by formulating this as a constrained optimization problem. We compare our algorithm with an existing 5-point method, and show our formulation to be more robust in the presence of noise.
Publication:
(Poster) Dhruv Batra, Bart Nabbe, and Martial Hebert. An Alternative Formulation for the Five Point Relative Pose Problem. IEEE Workshop on Motion and Video Computing 2007 (WMVC '07).
[ pdf ]