Overview
CacheBleed is a side-channel attack that exploits information leaks through cache-bank conflicts in Intel processors. By detecting cache-bank conflicts via minute timing variations, we are able to recover information about victim processes running on the same machine. Our attack is able to recover both 2048-bit and 4096-bit RSA secret keys from OpenSSL 1.0.2f running on Intel Sandy Bridge processors after observing only 16,000 secret-key operations (decryption, signatures). This is despite the fact that OpenSSL's RSA implementation was carefully designed to be constant time in order to protect against cache-based (and other) side-channel attacks.
While the possibility of an attack based on cache-bank conflicts has long been speculated, this is the first practical demonstration of such an attack. Cache-bank conflicts have been documented since at least 1996. (See, for example, Agner Fog's How to Optimize for the Pentium Processor.) However, these were not widely thought to be exploitable, and as a consequence common cryptographic software developers have not implemented countermeasures to this attack.
Paper
Latest version can be downloaded here.Q&A
Q1: Which software versions are vulnerable?
OpenSSL: Our attack code has been tested with OpenSSL 1.0.2f. We believe that all OpenSSL versions from 0.9.7h up to and including versions 1.0.1r and 1.0.2f are vulnerable.
LibreSSL: We have verified that version 2.3.1 is vulnerable. We believe that all LibreSSL versions, up to and including 2.1.9, 2.2.5 and 2.3.1 are vulnerable.
NSS: A code review of NSS 3.21 indicates that it is likely to be vulnerable.
Q2: Which ciphers are affected?
Our attacks targets OpenSSL's implementation of RSA (both RSA decryption as well as RSA signatures). Although we have not demonstrated this, in principle our attack should be able to leak partial information about ElGamal encryption as well.
Q3: Which processor versions are vulnerable?
We performed our tests on an Intel Xeon E5-2430. We believe that all Sandy Bridge processors are vulnerable. Earlier microarchitectures, such as Nehalem and Core 2 may be vulnerable as well.
Our attack code does not work on Intel Haswell processors, where, apparently, cache-bank conflicts are no longer an issue. (See Intel Optimization Manual)
Q4: When will patches be available?
We disclosed our attack to OpenSSL's development team in early January and it was assigned CVE-2016-0702. We have also collaborated with OpenSSL's team by suggesting suitable countermeasures and verifying their effectiveness. OpenSSL released an update on March 1, 2016 containing these countermeasures. These updated versions are not vulnerable to our attacks. The developers of BoringSSL informed us that they will incorporate the OpenSSL changes into their product. The developers of LibreSSL are working on a fix but do not have a timeline yet. We have disclosed these results to the developers of the NSS library in early January. We do not know when a fix will be deployed.Q5: Should normal users or system administrators be worried?
OpenSSL has classified this vulnerability as "low severity", which we agree with. In order to mount the attack, the attacker has to be able to run the attack code on the same machine that runs the victim code. CacheBleed is a complex attack and there are much easier-to-exploit vulnerabilities in personal computers that it is unlikely that anyone would use CacheBleed in such an environment.
Cloud servers that commonly run mutually untrusting workloads concurrently are a more realistic attack scenario. A malicious client of a cloud service could use the CacheBleed attack to spy on other clients. While cloud servers employ techniques to isolate workloads of different clients from one another, these techniques only isolate the software and do not prevent hardware-based attacks, such as CacheBleed. Nevertheless, due to the complexity of the attack and its sensitivity to system noise we believe it is not currently a practical risk to cloud environments.
The attack only works between processes running on two hyper-threads of the same core. Disabling hyper-threading is an effective mitigation against the attack.
Q6: What countermeasures should developers take to protect against this attack?
Developers of cryptographic software should use a constant-time implementation. Constant-time implementations ensure that secret information is not disclosed through the operation of the code. For software to be constant time it should be written such that:
- It only uses fixed-time instructions with arguments that depend on secret data
- It does not use conditional branches that depend on secret data
- It does not use memory access patterns that depend on secret data
Q7: What is the cache?
Over the years, memory speed has not kept pace with the speed of the processor. To bridge the speed gap, processor designs include caches which are small banks of memory that store the contents of recently accessed memory locations. Caches are much faster (up to two orders of magnitude) than main memory, because they are smaller and closer to the processor. On modern CPUs there are several levels of cache hierarchy, with each level being larger than the previous at the expense of being slower.
Cache Hierarchy
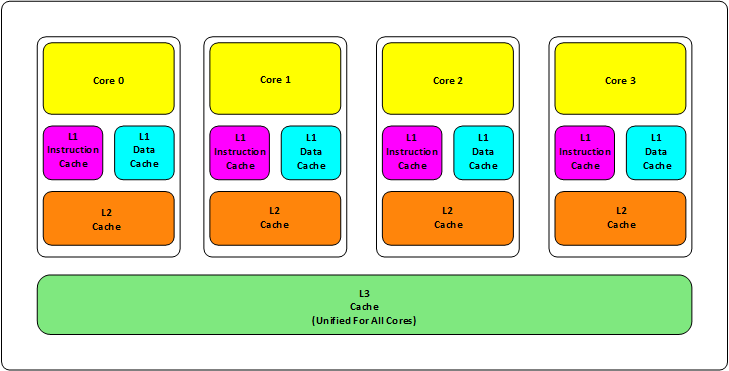
Each cache is divided into fixed-size blocks called lines. When a CPU core accesses a memory location, the corresponding line is fetched from the lowest cache level containing it among the caches belonging to the same core. If the value is not contained in any of the cache levels, it is loaded into the cache from the main memory. Further access to memory addresses within the line will be served from the cache, reducing the time the processor needs to wait for the data to become available.
Q8: How do cache timing attacks work?
Cache timing attacks exploit timing differences between accessing cached vs. non-cached data. Since accessing cached data is faster, a program can check if its data is cached by measuring the time it takes to access it.
In one form of a cache timing attack, the attacker fills the cache with its own data. When a victim that uses the same cache accesses data, the victim's data is brought into the cache. Because the cache size is finite, loading the victim's data into the cache forces some of the attacker's data out of a cache. The attacker then checks which sections of its data remain in the cache, deducing from this information what parts of the victim's memory were accessed.
Q9: What are cache-bank conflicts?
To facilitate access to the cache and to allow concurrent access to the L1 cache, cache lines are divided into multiple cache banks. On the processor we tested, there are 16 banks, each four bytes wide. The cache uses bits 2-5 of the address to determine the bank that a memory location uses.
In the Sandy Bridge microarchitectures, the cache can handle concurrent accesses to different cache banks, however it cannot handle multiple concurrent accesses to the same cache bank. A cache-bank conflict occurs when multiple requests to access memory in the same bank are issued concurrently. In the case of a conflict, one of the conflicting requests is served immediately, whereas other requests are delayed until the cache bank is available.
Q10: How does CacheBleed detect cache-bank conflicts?
CacheBleed issues a long sequence of read requests to memory addresses in a single cache bank and measures the time it takes to serve all of these requests. This time depends on many factors, one of which is the number of cache-bank conflicts. The diagram below shows histograms of the time to read 256 memory locations under several scenarios. (All examples taken on an Intel Xeon E5-2430 processor.)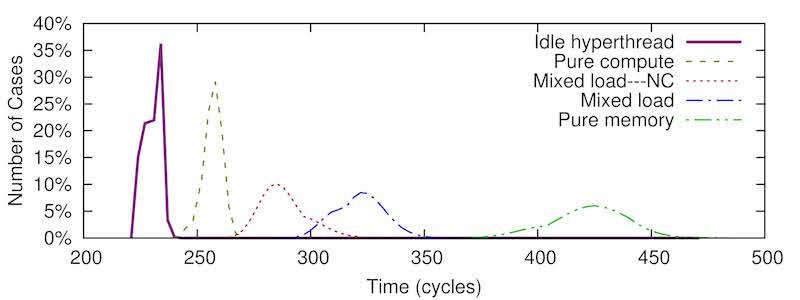
As we can see, when the measurements are taken when only one hyper-thread is active, access is quick (230 cycles). When measurements are taken on one hyper-thread when the other hyper-thread consistently accesses the monitored cache bank, access is much slower (around 420 cycles). When the monitored hyper-thread uses a mixed load (in this example one memory access for each three computation operations), we can see that the average measurement on the cache bank the monitored hyper-thread accesses is 325 cycles, whereas the average measurement on other cache banks is 280. The smaller the difference between access patterns to different cache banks is, the closer the measured distributions are.
Q11: Which part of the OpenSSL's implementation leaks secret information?
The main operation OpenSSL performs when decrypting or signing using RSA is modular exponentiation. That is, it calculates where d is the private key. To compute a modular exponentiation, OpenSSL repeatedly performs five squaring operations followed by one multiplication. The multiplier in the multiplications is one of 32 possible values. All the numbers involved in these operations are half the size of the key. That is, for a 2048 bit RSA key, the numbers are 1024 bits long.
Knowing which multiplier is used in each multiplication reveals the secret exponent and with it the private key. Past cache timing attacks against OpenSSL and GnuPG recover the multipliers by monitoring the cache lines in which the multipliers are stored. To protect against such attacks, OpenSSL stores the data of several multipliers in each cache line, ensuring that all of the cache lines are used in each multiplication. However, the multipliers are not spread evenly across cache banks. Instead, they are divided into 8 bins, each bin spanning two cache banks. More specifically, multipliers 0, 8, 16 and 24 only use bin 0, which spans cache banks 0 and 1. Multipliers 1, 9, 17, and 25 only use bin 1, which spans cache banks 2 and 3, etc. As a result of this memory layout, each multiplication accesses two cache banks slightly more than it accesses the other cache banks. For example, in the case of 4096-bit RSA, the multiplication makes 128 additional accesses to the multiplier's cache banks.
Q12: What does the leakage look like?
Our attack code monitors the use of a cache bank throughout the modular exponentiation. It repeatedly measures the time to access the monitored cache bank using the procedure we describe in the answer to Q10 above. By repeating the process for each even cache bank we get traces of the use of each cache bank during the exponentiation. (Recall that each bin occupies two cache banks hence even and odd cache banks show similar access patterns.)
As discussed above, there is only a small difference between the number of victim access to the cache bank used for the multiplier and the number of accesses to other cache banks. Consequently, the distributions of our measurement results are very similar and a single measurement does not provide accurate information on the number of victim accesses to the cache bank. To get more accurate results, we collect 1,000 traces of measurements for each even cache bank, and average these traces. The results of this are shown in the diagram below.
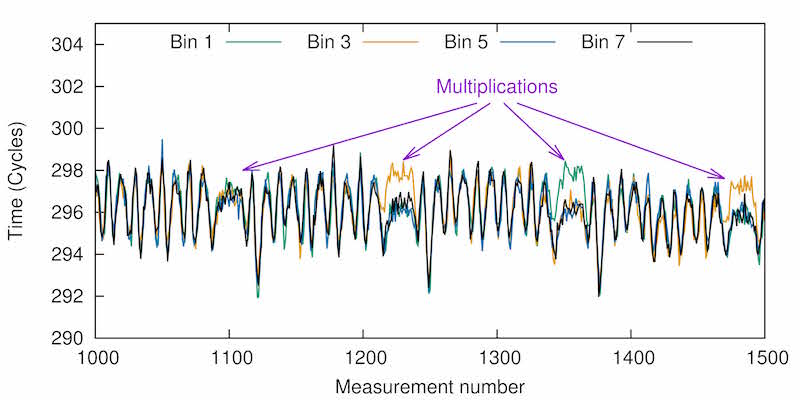
The graph shows the average measurement times for the four odd bins and covers a span of 4 multiplications (marked). Between the multiplications we can observe the squaring and modular reduction operations. In the second and fourth multiplication we see that bin 3 is more active than the others, indicating that the multiplier used in each of these multiplications is one of 3, 11, 19 and 27. Similarly, in the third multiplication bin 1 is more active, infdicating that the multiplier is one of 1, 9, 17, 25.
The leaked information reduces the number of options for each multiplication from 32 to 4. Hence, using CacheBleed we are able to recover 60% of the key material of the private key.
Q13: How do you find the missing bits?
RSA keys contain a lot of redundancy. Multiple techniques have been developed for recovering the key from partial key material. In our work we adapt the Heninger-Shacham algorithm to the data on the Chinese remainder coefficients that CacheBleed leaks.
Recovering a 4096 RSA key from 60% of the key material requires around two CPU hours and can be accomplished on a high-end server in less than 3 minutes.
Acknowledgments
NICTA is funded by the Australian Government through the Department of Communications and the Australian Research Council through the ICT Centre of Excellence Program.This material is based upon work supported by the U.S. National Science Foundation under Grants No. CNS-1408734, CNS-1505799, and CNS-1513671, and a gift from Cisco. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the authors and do not necessarily reflect the views of the U.S. National Science Foundation.
This work was sponsored by the Blavatnik Interdisciplinary Cyber Research Center; Check Point Institute for Information Security; by a Google Faculty Research Award; by the Israeli Centers of Research Excellence I-CORE Program (center 4/11); by the Leona M. & Harry B. Helmsley Charitable Trust; and by NATO's Public Diplomacy Division in the Framework of "Science for Peace".