CS 3451, Spring 2012

Homework 1: Transformations and Projection

Due: 11:55pm, Monday, February 6, 2012

Objective

The goal of this assignment is to write the routines that allow a user to transform and view 3D graphical objects. In particular, you will write the routines for creating line drawings of both orthographic and perspective scenes. You will use Processing to write all of this code. The transformation routines that you create will implement a matrix stack and will allow you to arbitrarily rotate, translate and scale an object. To make this assignment easier, routines will be provided for you that implement line clipping and line drawing. The images that you create for this exercise will be three dimensional line drawings of scenes with no hidden surfaces or filled polygons. All of the lines will be uniformly white so that you will not need to perform color interpolation.

Routines You Will Create

In this assignment you will be creating routines that mimic the behavior of several OpenGL library routines. Below is the list of routines that you will create for this assignment.

gtInitialize()

The gtInitialize command should initialize your matrix stack to have just a single matrix on the stack. This matrix should be the identity matrix.

gtPushMatrix(), gtPopMatrix()

The gtPushMatrix command replicates the matrix at the top of the matrix stack and places this new matrix on top of the stack. This new top matrix is now the current transformation matrix. The gtPopMatrix command pops the top matrix off the stack, causing the next matrix down to become the current transformation matrix. An error message should be printed if a pop is attempted when only one matrix is on the stack. As described under the gtInitialize command, the matrix stack is initially created with an identity matrix as the only matrix on the stack. Your stack only needs to handle up to 10 matrices on it at any one time.

gtTranslate(float tx, float ty, float tz)

Multiply the current transformation matrix on the right by a matrix specifying a translation of (tx, ty, tz). The current transformation matrix is defined to be the top matrix on the matrix stack.

gtScale(float sx, float sy, float sz)

Multiply the current transformation matrix on the right by a matrix specifying a (possibly non-uniform) scaling of (sx, sy, sz).

gtRotate(float angle, float ax, float ay, float az)

Multiply the current transformation matrix on the right by a matrix that specifies a rotation of "angle" degrees about the axis (ax, ay, az). The rotation is counter-clockwise as one looks from the position (ax, ay, az) towards the origin. For example, the command gtRotate (30.0, 1.0, 0.0, 0.0) specifies a 30 degree rotation counter-clockwise around the x-axis.

gtOrtho(float left, float right, float bottom, float top, float near, float far)

Specifies that a parallel projection will be performed on subsequent vertices. The direction of projection is assumed to be along the z-axis. The six values passed to this routine describe a box to which all lines will be clipped. The "left" and "right" values specify the minimum and maximum x values that will be mapped to the left and right edges of the framebuffer. The "bottom" and "top" values specify the y values that map to the bottom and top edges of the framebuffer. The "near" and "far" values specify the nearest and farthest z values that will be drawn. The eye point is assumed to be facing the negative z-axis, so the "near" and "far" values actually define clipping planes along negative z.

gtPerspective(float fov, float near, float far)

Specifies that a perspective projection will be performed on subsequent vertices. The center of projection is assumed to be the origin, and the viewing direction is along the negative z-axis. The value "fov" is an angle in degrees that describes the field of view. In order to make it easier to write this routine, we will assume that all screen sizes will be square, so you don't need to worry about the vertical and horizontal field-of-view being different. The "near" and "far" values specify the locations along the negative z-axis at which to perform near and far clipping in z (just as in the gtOrtho command).
OpenGL uses a separate matrix to do projection that is different than the current transformation matrix and its associated stack. This means that in OpenGL, you can specify projections at any time before you draw lines and polygons. We will do the same for our assignment. Which ever projection that you specify (gtOrtho or gtPerspective) should be the last transformation that is applied to the line endpoints, regardless of where those procedure calls appear with respect to other transformations.
gtBegin(GT_LINES), gtEnd(), gtVertex3f(float x, float y, float z)

The gtBegin and gtEnd commands signal the start and end of a list of endpoints for line segments that are to be drawn. Each call to the routine gtVertex3f between these two commands specifies a 3D vertex that is a line endpoint. White lines are drawn between successive odd/even pairs of these vertices. If, for example, the four vertices v1, v2, v3, v4 are given in four sequential gtVertex3f commands then two line segments will be drawn, one between v1 and v2 and another between v3 and v4.
The vertices of the lines are modified in turn by the current transformation matrix and then by which ever projection was most recently described (gtOrtho or gtPerspective). Only one of gtOrtho or gtPerspective is in effect at any one time. These projections do not affect the matrix stack and the current transformation matrix. Your gtBegin, gtVertex3f and gtEnd commands must be able to draw any number of lines. You should draw the lines as soon as both vertices are given to you (using gtVertex3f), so there is no need to store more than two vertex positions at any time.

Code Provided

Two routines will be provided for you that will perform the necessary clipping and drawing of lines. This means that there is no need for you to write any clipping or line drawing code. These routines are:

near_far_clip(near, far, p0, p1)

This routine clips the line from (p0.x, p0.y, p0.z) to (p1.x, p1.y, p1.z) to the specified "near" and "far" clip distances along the z-axis. The "near" and "far" values are floats. The parameters p0 and p1 are of the class "xyz" (triplets of floats) so that they may be altered by the routine. (Example of declaring and initializing an xyz object: "xyz mypoint = new xyz(1.0, 1.5, 2.5);". Example of assigning values to an xyz object: "mypoint.x = 12.9;". See the file "lines.pde" for the class declaration.) This routine returns a value of 1 if at least part of the line is visible, and 0 if it is entirely outside the window. DO NOT DRAW THE LINE IF THIS ROUTINE RETURNS 0.

draw_line(float x0, float y0, float x1, float y1)

This routine draws a white line from (x0, y0) to (x1, y1). The coordinates are 2D pixel coordinates for the currently defined framebuffer. If, for example, the framebuffer is 100 pixels wide, the left edge of the screen is x = 0 and the right is x = 100. This routine performs clipping to the framebuffer window.

All these library routines can be downloaded here: hw1_stub_ldraw.zip

What You Will Write

You will write code ONLY in the file matlib.pde. All of your routines should be contained in matlib.pde. We have provided a "dummy" version of matlib.pde that you can use as a starting point for creating your own complete version.

All test samples have already been contained in the provided code. Pressing keyboard keys 1-9 and 0 calls the 10 test samples respectively.

Suggested Approach

First, become familiar with using the draw_line routine. Second, implement the matrix stack and the gtTranslate and gtScale commands. Test them out by applying the current transformation matrix to the line endpoints and then just draw lines by ignoring the z-values. Third, write the gtOrtho command. This should be fairly straightforward once you have already drawn some lines by ignoring the z-values of the transformed vertices. Fourth, implement the gtPerspective command. The best way to test out this routine is to carefully work out some simple test cases on paper and match the execution of your code with these worked-out examples. Finish by implementing the gtRotate command. Logically this command should be implemented together with gtScale and gtTranslate, but it is a little tricker. You will need to create and manipulate matrices and vertices in order to implement the transformation routines. Here are possible definitions:

class gtMatrix {
  float[][] m;
  gtMatrix() {m = new float[4][4];}
}

class gtVertex {
  float[] v;
  gtVertex() {v = new float[4];}
}

Because the last row of a typical transformation matrix is 0 0 0 1, you may instead choose to use 4 by 3 matrices. You may also decide not to store the implicit 1 that is the fourth element of a homogeneous coordinate of a vertex. Two important routines that you will need to write are matrix-matrix multiplication and matrix-vector multiplication. Your choices of data structures will affect the details of these routines.

You will probably write routines that perform operations such as matrix multiply and vector cross-product. It is easy to accidentally write a routine that clobbers some of the results if the routine is called using the same matrix more than once. For example, the invocation "mult_matrices (a, b, b)" is meant to multiply a time b and put the result in b. If you are not careful, however, you will overwrite part of b before you use all of the values in that matrix. The best way to avoid this is to place all your results in a temporary matrix and then copy the results to the final destination when you are finished.

Authorship Rules

The code that you turn in entirely your own. You are allowed to talk to other members of the class and to the Professor and the TA about general implementation of the assignment. It is, for example, perfectly fine to discuss how one might organize the data for a matrix stack. It is also fine to seek the help of others for general Processing/Java programming questions. You may not, however, use code that anyone other than yourself has written. Code that is explicitly not allowed includes code taken from the Web, from books, from previous assignments or from any source other than yourself. The only exception to this rule is that you should use the GT Graphics Library routines and the test code that we provide. You may NOT use other library routines for matrices and stacks. You should not show your code to other students. Feel free to seek the help of the Professor and the TA's for suggestions about debugging your code.

Development Environment

You must use the Processing language which is built on Java. The best resource for Processing language questions is the online or offline Processing language API (found in the "reference" subdirectory of the Processing release).

Sample Results

pic01.jpg pic02.jpg pic03.jpg pic04.jpg pic05.jpg pic06.jpg pic07.jpg pic08.jpg pic09.jpg pic10.jpg
All 10 results zipped: hw1_results_png.zip

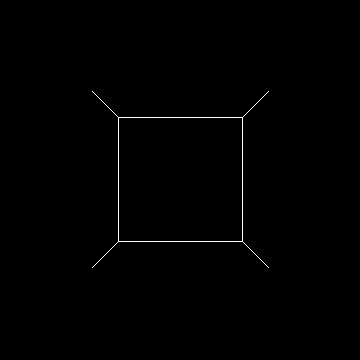
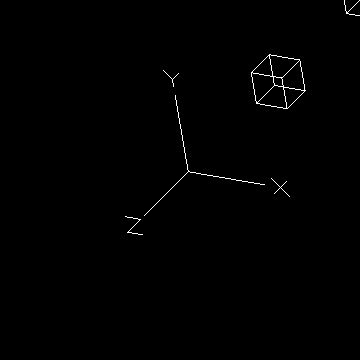
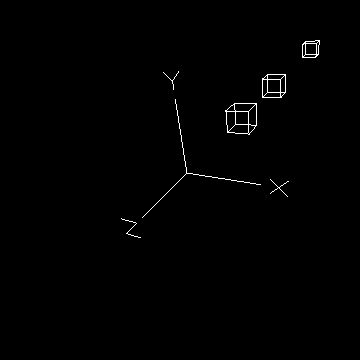
What To Turn In

Compress the whole folder (not merely the files within the folder) into a zip archive and submit it in T-square for Project 1. The zip archive should be included as an attachment. The filename should be "lastname_firstname_project_1.zip". For example, Greg Turk would create "turk_greg_project_1.zip" for his homework 1. When unzipped, it will produce the folder "ldraw" containing the files "ldraw.pde", "gtGraphics.pde", "lines.pde", and "matlib.pde".