

















We provide a skeleton Processing for you to begin with: meshes.zip This code provides a routine to parse the keyboard commands. It also contains the start of a routine for reading in a mesh file. You will modify this mesh reading routine to store the mesh in a data structure of your own choosing.
The file format we will use for this project is a simple text format for meshes. The file format is basically an indexed face set. The first two lines specify the number of vertices and faces of the model, respectively. Then all of the vertex (x,y,z) values are listed, one per line. This is followed by the list of faces, one face per line. The first number that describes a face is simply the number of sides of that face, and for this project, that number will always be 3. Following this, indices into the vertex list are given. The vertices are indexed starting from the value zero.
Your finished program will be able to read a mesh from a file and display that mesh. More importantly, with a keystroke your program will create the triangulated dual of that mesh and display the resulting new mesh. Your program should also allow toggling between flat shading (per-polygon normals) and smooth shading (per-vertex normals). Your program should obey the following keystroke commands:
1-5: Read in a mesh file (tetrahedron, octahedron, icosahedron, star, torus).
d: Calculate the triangulated dual of the current mesh.
n: Toggle between per-face and per-vertex normals.
r: Assign a random color to each face of the mesh. (Set colors once - don't make flickering colors!)
w: Change the colors of the mesh faces to white.
space: Toggle automatic rotation on and off.
 |  |  |
 |
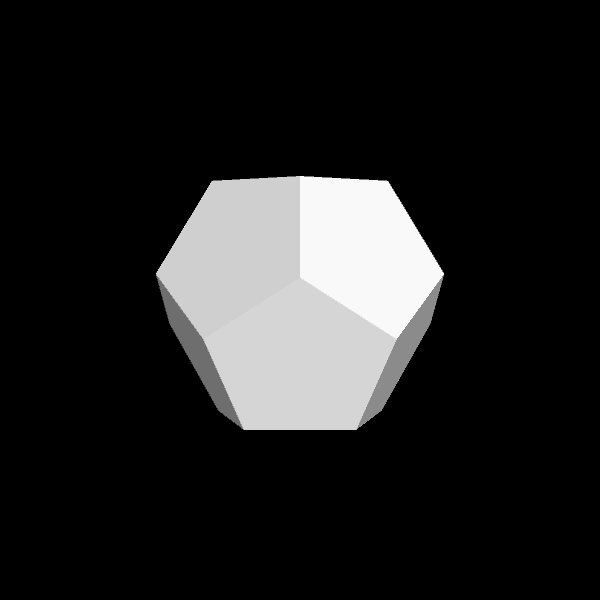
| Original flat-shaded tetrahedron | Original smooth-shaded tetrahedron | Dual | Dual with random colors |
 |  |  |
 |
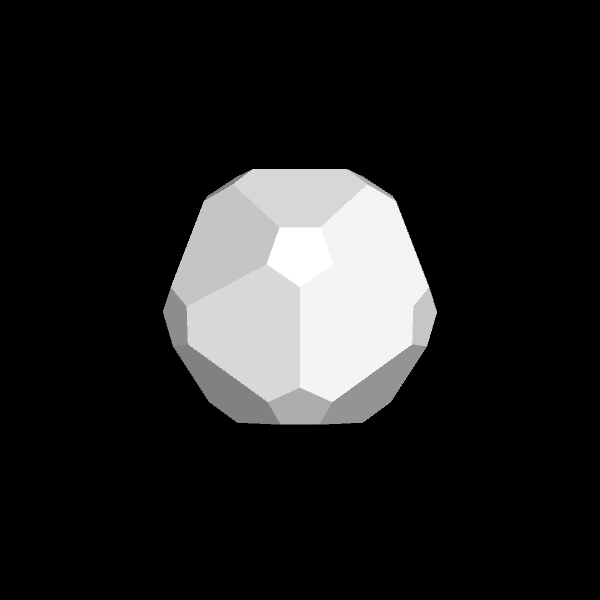
| Original flat-shaded octahedron | Original smooth-shaded octahedron | Dual | Dual with random colors |
 |  |  |
 |
| Original flat-shaded icosahedron | Original smooth-shaded icosahedron | Dual | Dual with random colors |
 |  |  |
 |
| Original flat-shaded star | Original smooth-shaded star | Dual | Dual with random colors |
 |  |  |
 |
| Original flat-shaded torus | Original smooth-shaded torus | Dual | Dual with random colors |
First, modify the skeleton code to read in the .ply file format into your own polyhedral model data structure. Next, modify the "draw" routine to draw the current polyhedral mesh. You can then write the code needed to calculate surface normals at the vertices of a model. Modify the drawing routine so that it can toggle between per-face and per-vertex normals. Finally, write a routine that takes a given model and creates the triangulated dual of it.
Calculating the triangulated dual of a give mesh is perhaps the most challenging aspect of this project. There are several stages to doing this. First, you will want to calculate the centroid of each triangle. These triangle centroids will become some of the vertices in your dual mesh. Usually, you would then travel around a given vertex of the original mesh, connecting together these triangle centroids into a dual face. Unfortunately this would sometimes create faces with more than three edges, and we want to restrict this project to only triangles. To avoid this, you should triangulate a given dual face by calculating a new vertex that is the average of the triangle centroids. Then create the collection of new triangles that together form the dual face. Once you have created a new triangulated dual face for each vertex of the original mesh, you will have completed the triangulated dual mesh. See the octahedron and its triangulated dual in the images above to see how each original vertex is turned into a square, and how each square is in fact made of four triangles (shown by the random colors).
Note that you should be able to create the triangulated dual of a model more than once. Each time you calculate the dual, this will result in a mesh that has more triangles than the previous one.
We strongly recommend using the "corners" representation to store and manipulate your polygonal meshes. Note that all of the meshes for this project contain only triangles, so the corners representation is appropriate. Keep in mind that you will need mesh adjacency information to create a dual mesh and also to calculate per-vertex normals.
The code that you turn in must be entirely your own. You are allowed to talk to other members of the class and to the instructor and the TA about high-level questions about the assignment. It is also fine to seek the help of others for general Java/Processing programming questions. You may not, however, use code that anyone other than yourself has written. Code that is explicitly not allowed includes code taken from the Web, from books, or from any source other than yourself. The only exception to this is that you can make use of the sample Processing code that we have provided for this assignment. You should not show your code to other students. If you need help with the assignment, seek the help of the instructor or the TA.
Turn in all of your Processing source files (.pde) on T-square.