Shape Transformation Using Variational Implicit Functions
- Greg Turk and James F. O'Brien
- Georgia Institute of Technology
- (To appear in SIGGRAPH 99)
Abstract
Traditionally, shape transformation using implicit functions is performed in
two distinct steps: 1) creating two implicit functions, and 2) interpolating
between these two functions. We present a new shape transformation method
that combines these two tasks into a single step. We create a
transformation between two N-dimensional objects by casting this as a
scattered data interpolation problem in N+1 dimensions. For the case of 2D
shapes, we place all of our data constraints within two planes, one for each
shape. These planes are placed parallel to one another in 3D. Zero-valued
constraints specify the locations of shape boundaries and positive-valued
constraints are placed along the normal direction in towards the center of
the shape. We then invoke a variational interpolation technique (the 3D
generalization of thin-plate interpolation), and this yields a single
implicit function in 3D. Intermediate shapes are simply the zero-valued
contours of 2D slices through this 3D function. Shape transformation
between 3D shapes can be performed similarly by solving a 4D interpolation
problem. To our knowledge, ours is the first shape transformation method to
unify the tasks of implicit function creation and interpolation. The
transformations produced by this method appear smooth and natural, even
between objects of differing topologies. If desired, one or more additional
shapes may be introduced that influence the intermediate shapes in a
sequence. Our method can also reconstruct surfaces from multiple slices
that are not restricted to being parallel to one another.
PostScript version of paper. (4.3 Mbytes)
PDF version of paper (2.2 Mbtyes)
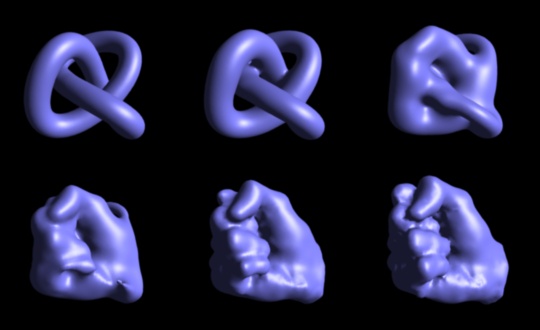 Knot to fist.
Knot to fist.
 Bunny to star.
Bunny to star.

Visualizing 2D shape tranformation as slices of a 3D surface.
Go to
Greg Turk's Home Page.
 Knot to fist.
Knot to fist.
 Knot to fist.
Knot to fist.
 Bunny to star.
Bunny to star.
