
Point sets obtained from computer vision techniques are often noisy and non-uniform. We present a new method of surface reconstruction that can handle such data sets using anisotropic basis functions. Our reconstruction algorithm draws upon the work in variational implict surfaces for constructing smooth and seamless 3D surfaces.
Implicit functions are often formulated as a sum of weighted basis functions that are radially symmetric. Using radially symmetric basis functions inherently assumes, however, that the surface to be reconstructed is, everywhere, locally symmetric. Such an assumption is true only at planar regions, and hence, reconstruction using isotropic basis is insufficient to recover objects that exhibit sharp features. We preserve sharp features using anisotropic basis that allow the surface to vary locally. The reconstructed surface is sharper along edges and at corner points. We determine the direction of anisotropy at a point by performing principal component analysis of the data points in a small neighborhood. The resulting surface is smoothed through tensor filtering.
We have applied the anisotropic basis functions to reconstruct surfaces from noisy synthetic 3D data and from real range data obtained from space carving.

Reconstruction from synthetic data using isotropic basis functions.

Reconstruction using anisotropic basis functions.

Data from voxel carving of the Ghirardelli Square model.
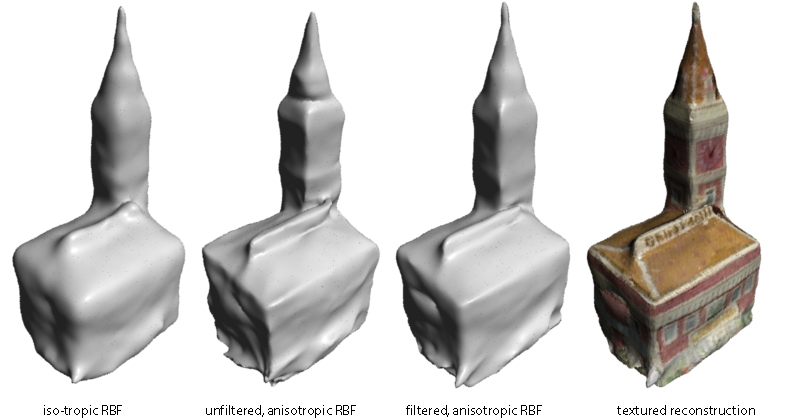
Comparison between isotropic, anisotropic and filtered anisotropic reconstructions.

Comparisons between two photos of the real model and the reconstructed images using anisotropic basis functions.
Go to Greg Turk's Home Page.