
copyright@planets_for

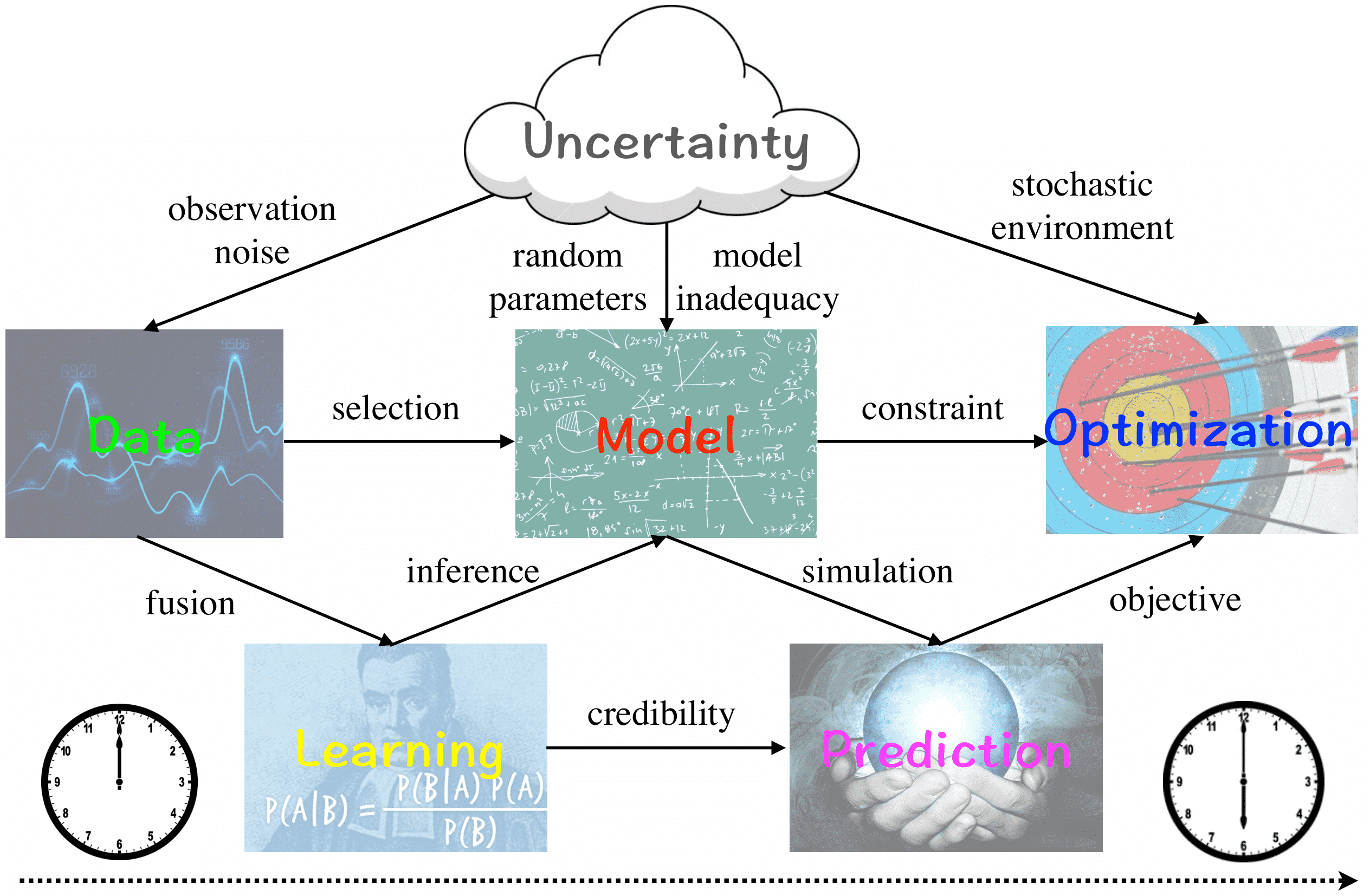
Our broad research interests are in the multidisciplinary fields of computational mathematics, data science, scientific machine learning, and parallel computing with various applications in computational science and engineering (CSE). Specifically, we are interested in developing fast, scalable, and parallel computational methods for integrating data and models under high-dimensional uncertainty to make (1) statistical model learning via Bayesian inference, (2) reliable system prediction with uncertainty quantification, (3) efficient data acquisition through optimal experimental design, and (4) robust control and design by stochastic optimization.
Predictive data and model integration by learning and optimization under uncertainty
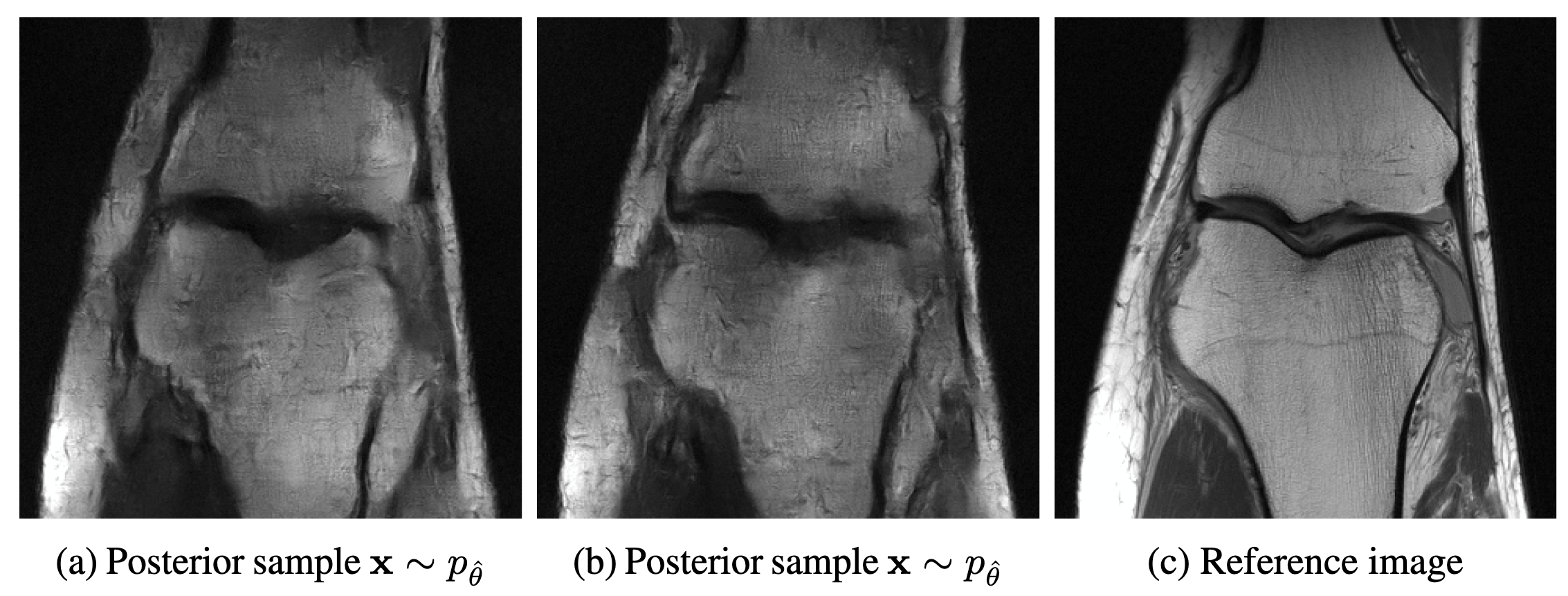
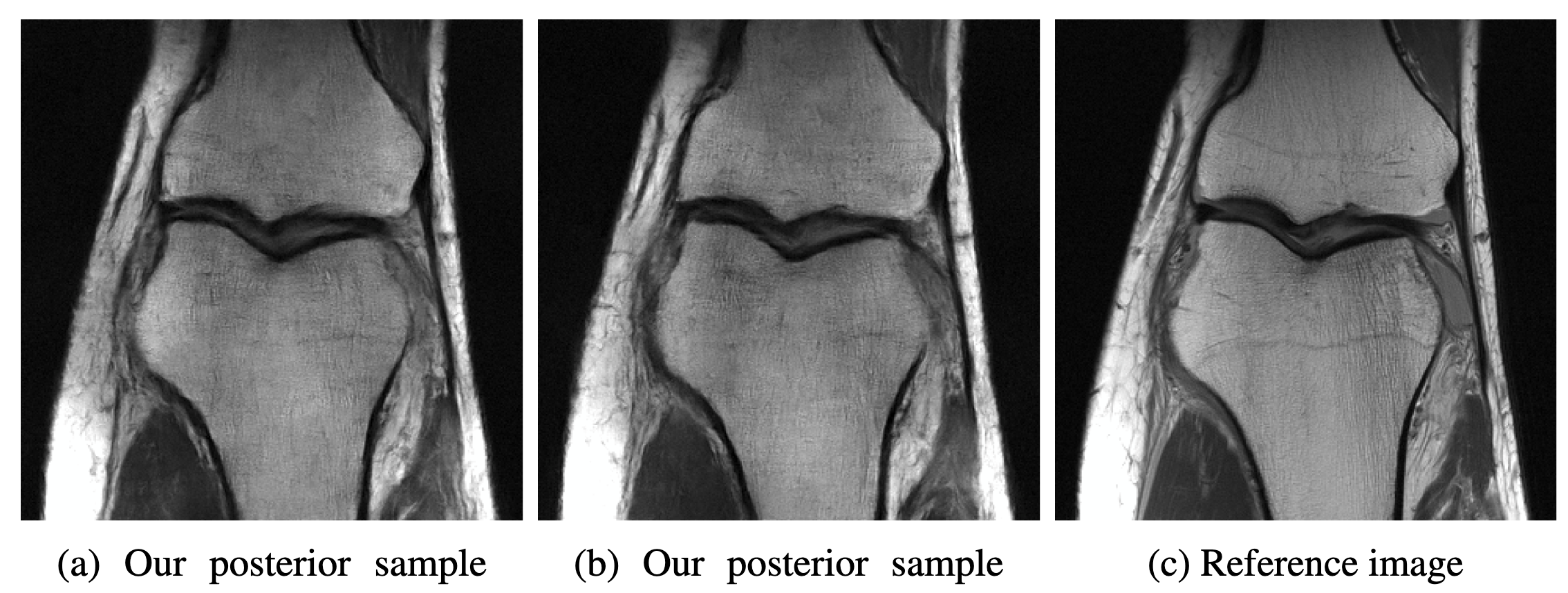
We develop novel Bayesian data assimilation methods, Latent-EnSF and LD-EnSF, which leverage diffusion model-based ensemble score filter with efficient and consistent latent representations of the full states and sparse observations to address the joint challenges of high dimensionality in states and high sparsity in observations for nonlinear Bayesian filtering, and achieve fast convergence, high accuracy and efficiency.
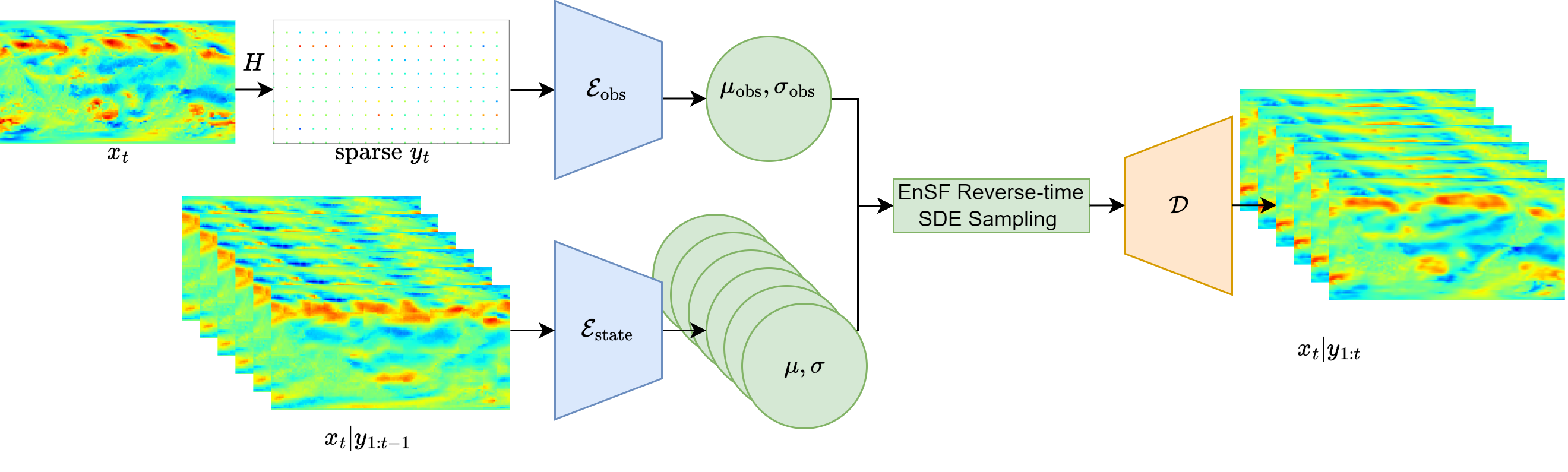
Flow of the Latent-EnSF. An ensemble of prior states \(x_{t}|y_{1:t-1}\) is assimilated with sparse observation \(y_{t}\) in the latent autoencoder space to obtain samples \(x_{t}|y_{1:t}\) from the posterior.
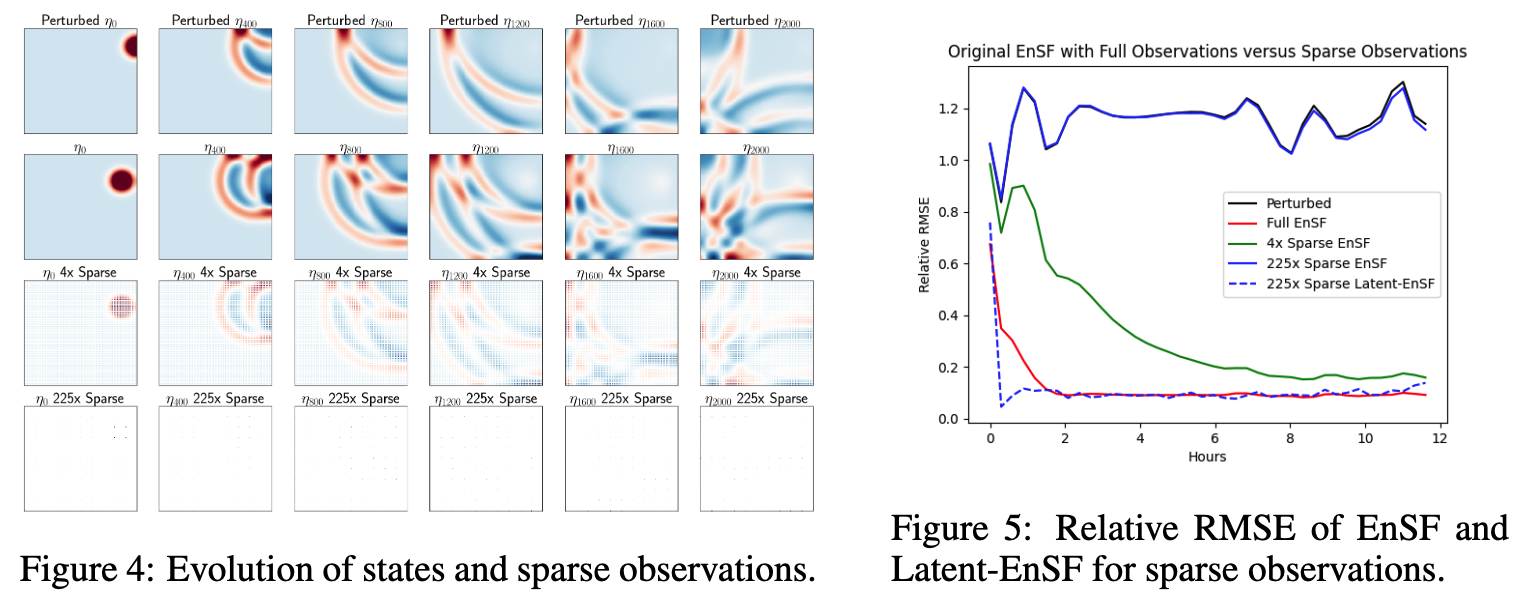

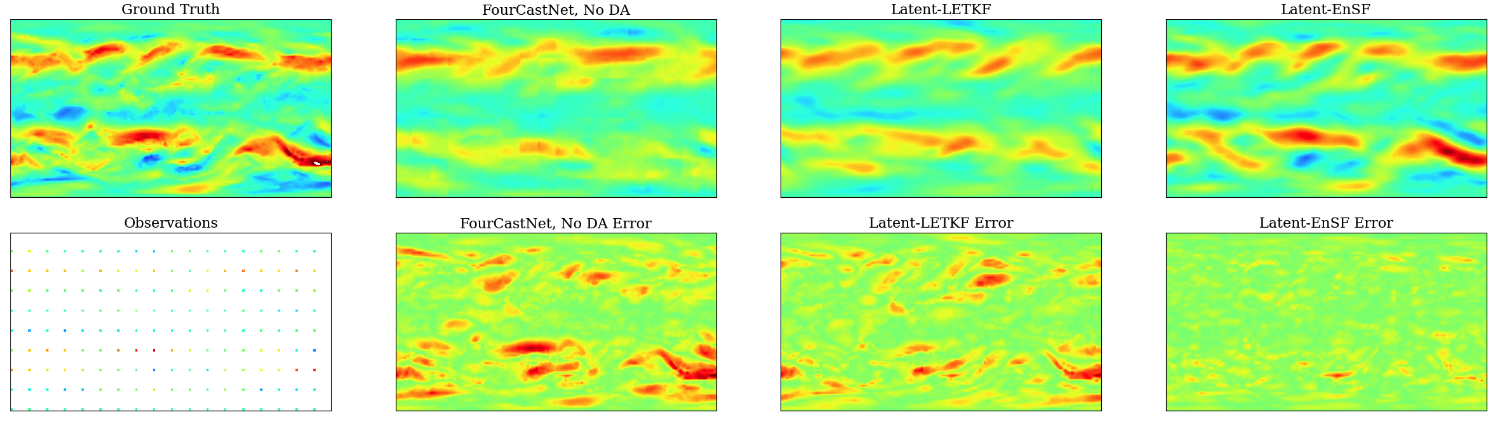
Latent ensemble score filter (Latent-EnSF) achieves faster convergence and higher accuracy compared to a few other methods for shallow water propagation and weather forecasting.

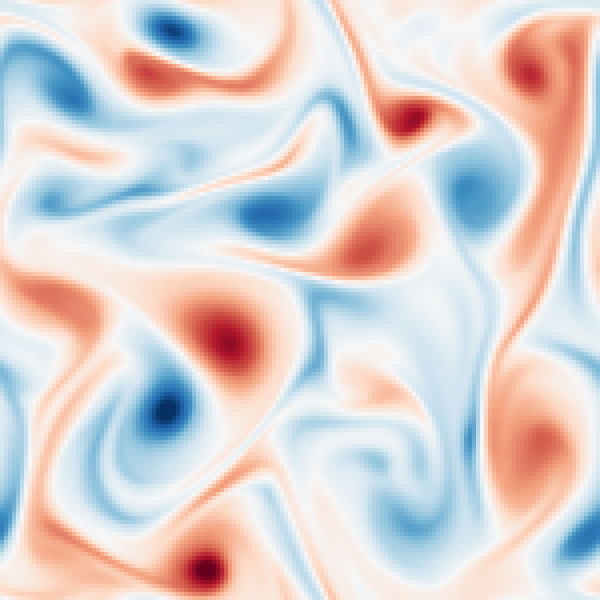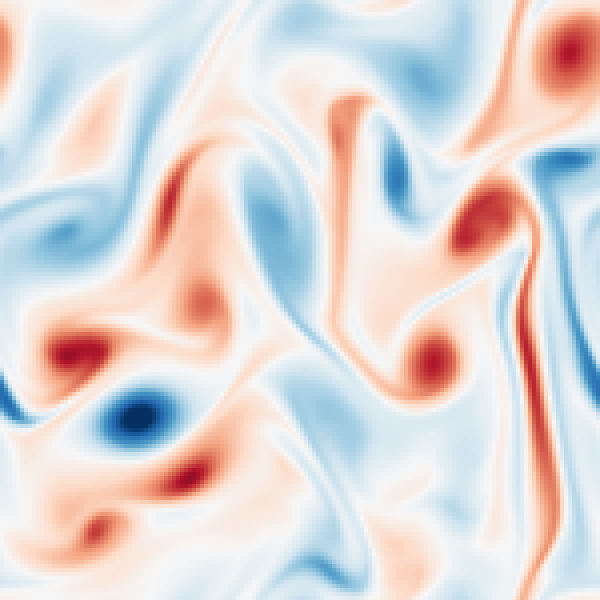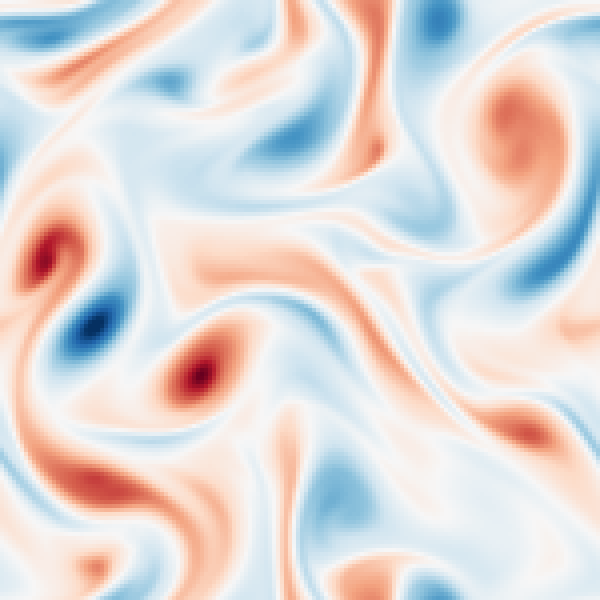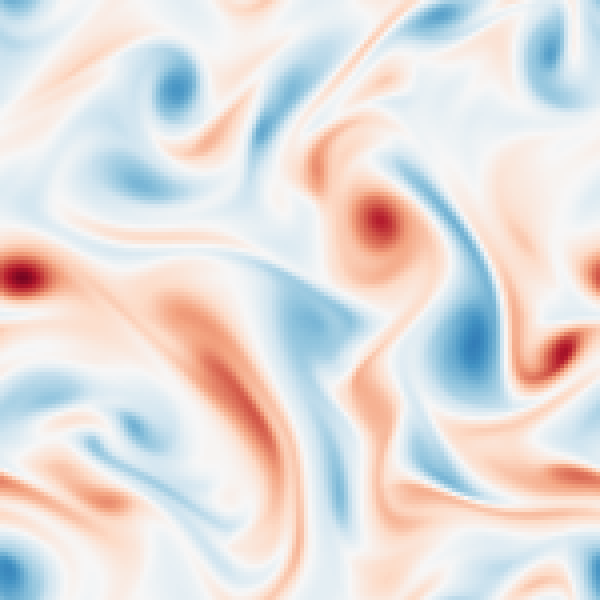

Flow of the LD-EnSF. An ensemble of historical sparse observations \(y_{1:i+1}\) is mapped (by LSTM) and assimilated (by EnSF) to the latent dynamics and decoded to the full dynamics.
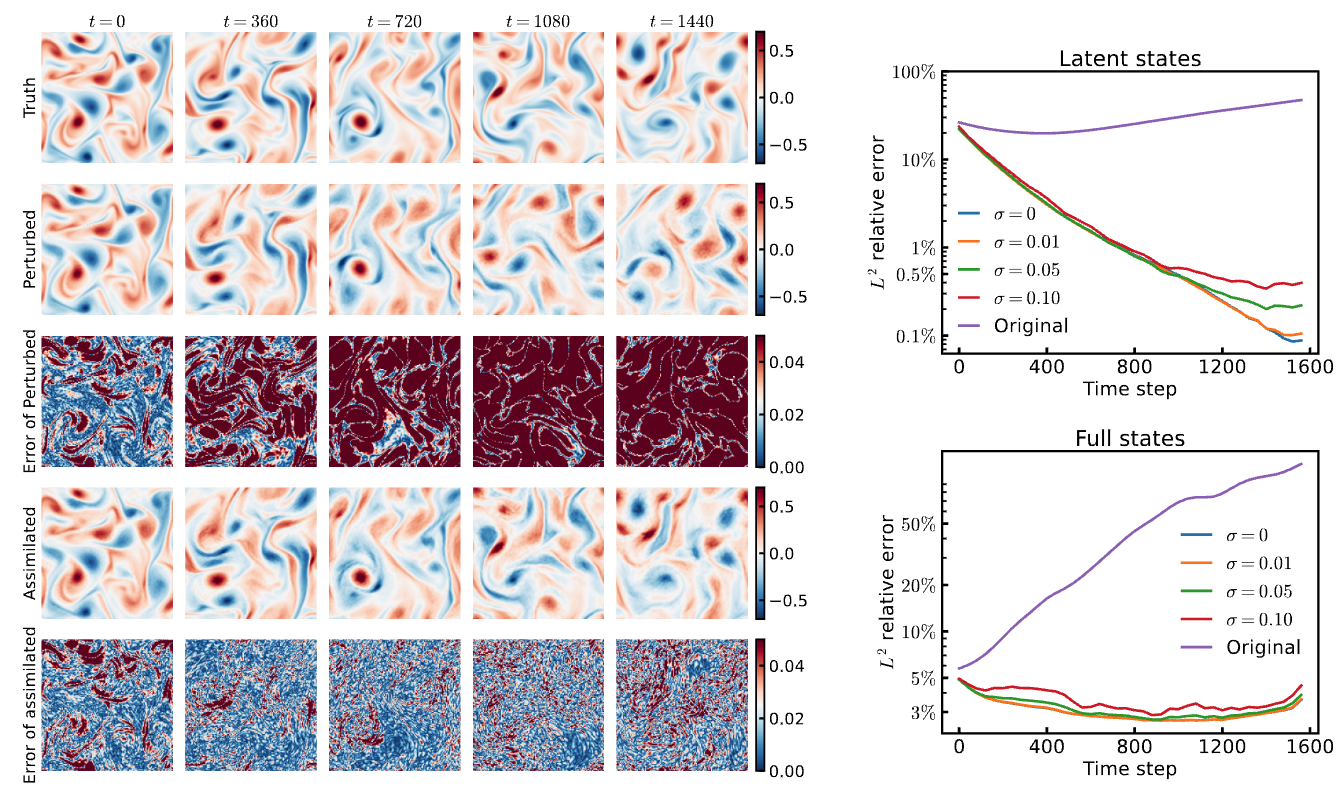
Assimilation of sparse observation of Kolmogorov flow to recover both the perturbed latent states and parameter (Reynolds number), which is accurately reconstructed to the full states.
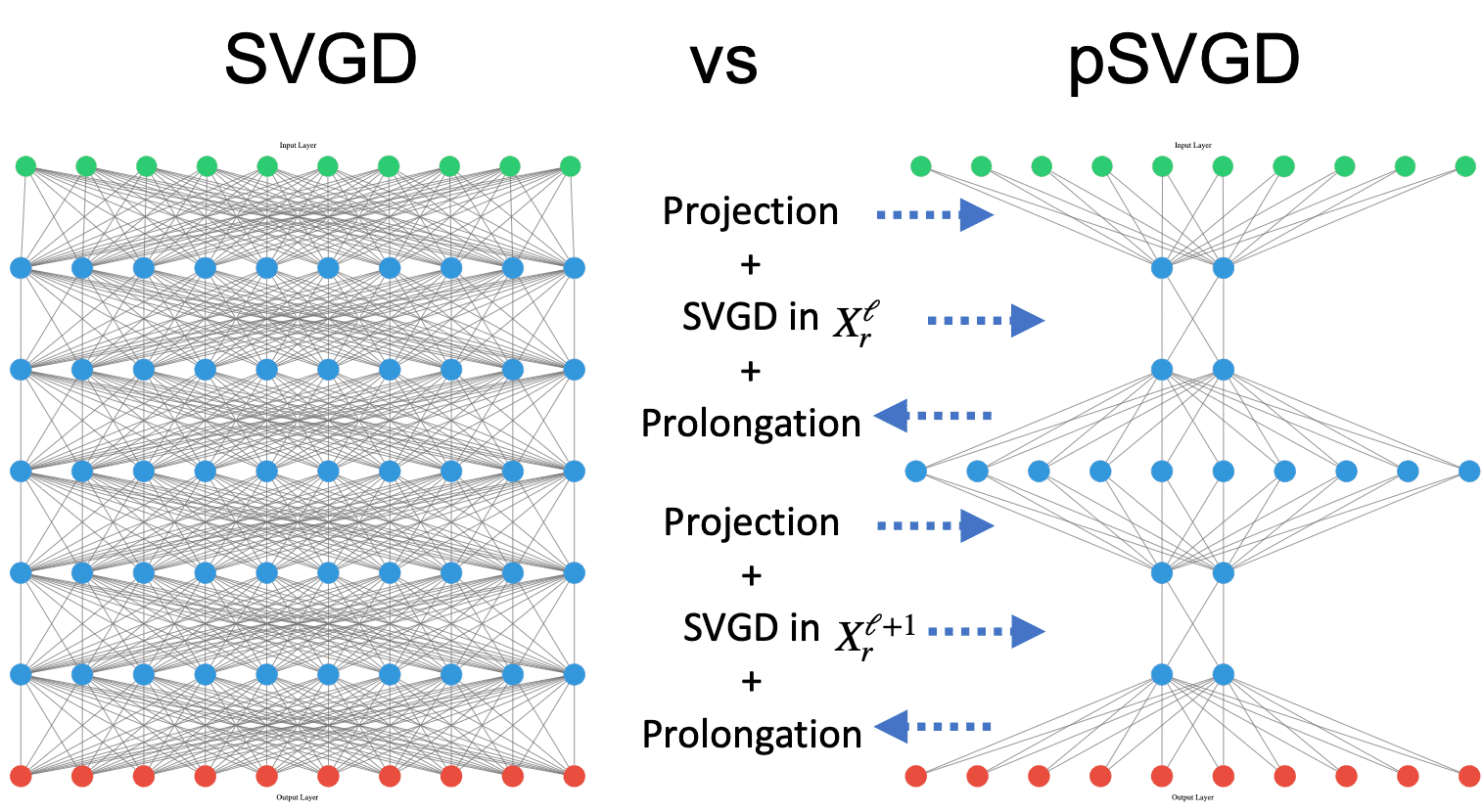
Project high-dimensional parameters to data-informed low-dimensional subspaces that are adaptively constructed using the gradient or Hessian of the parameter-to-observable map at current samples.
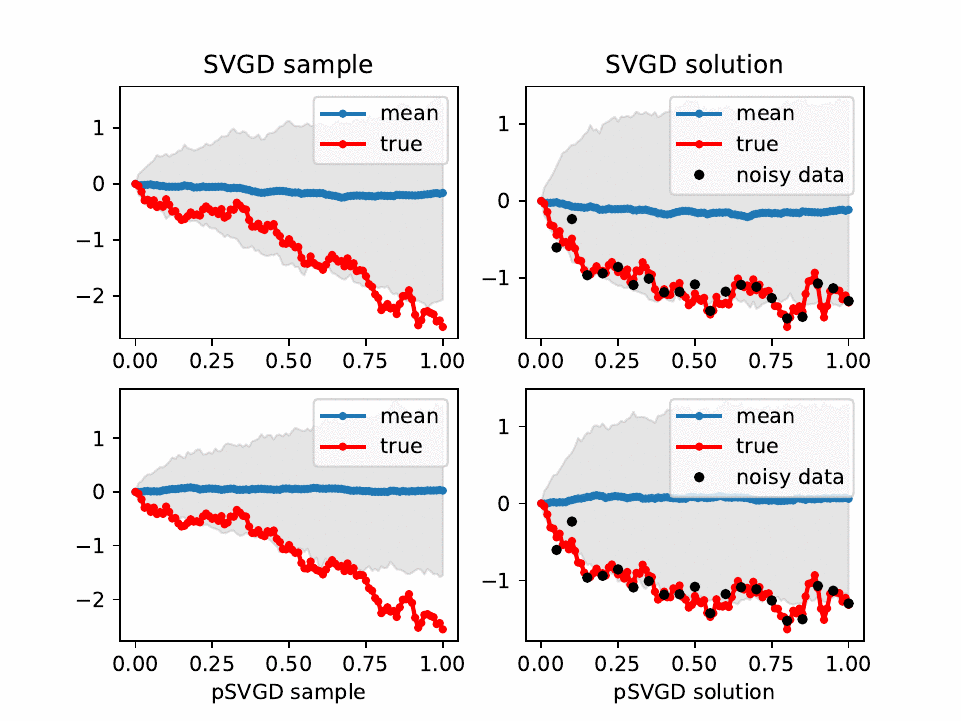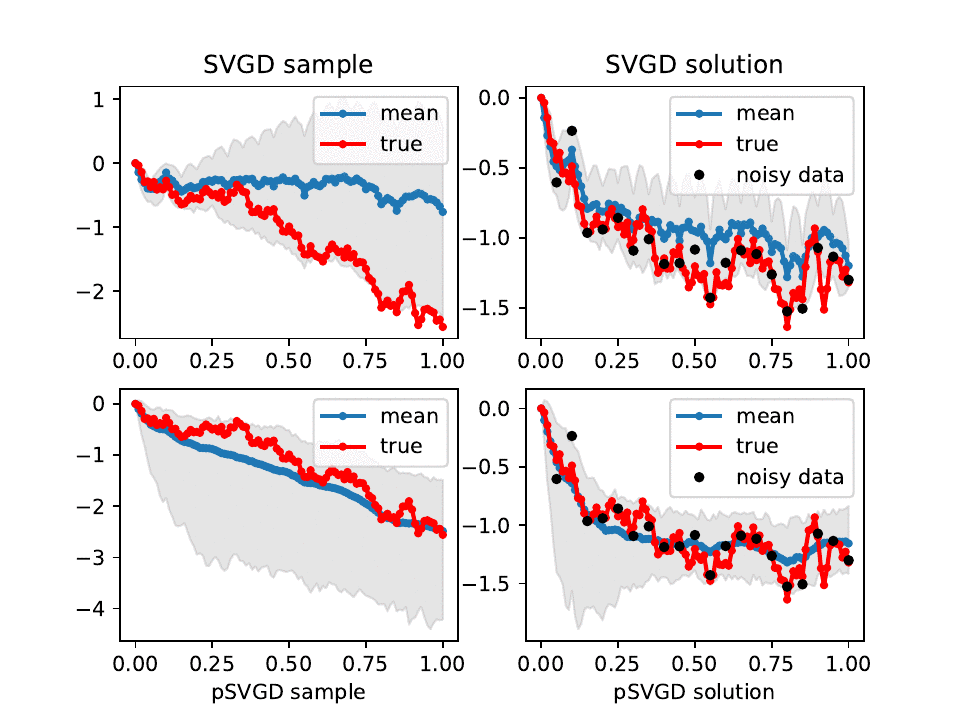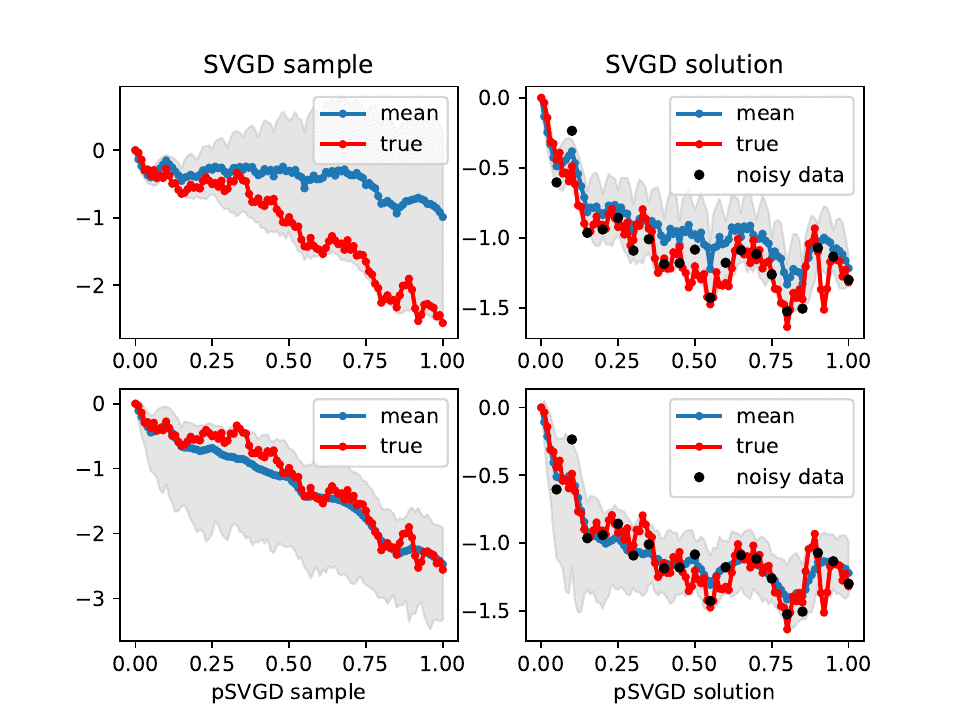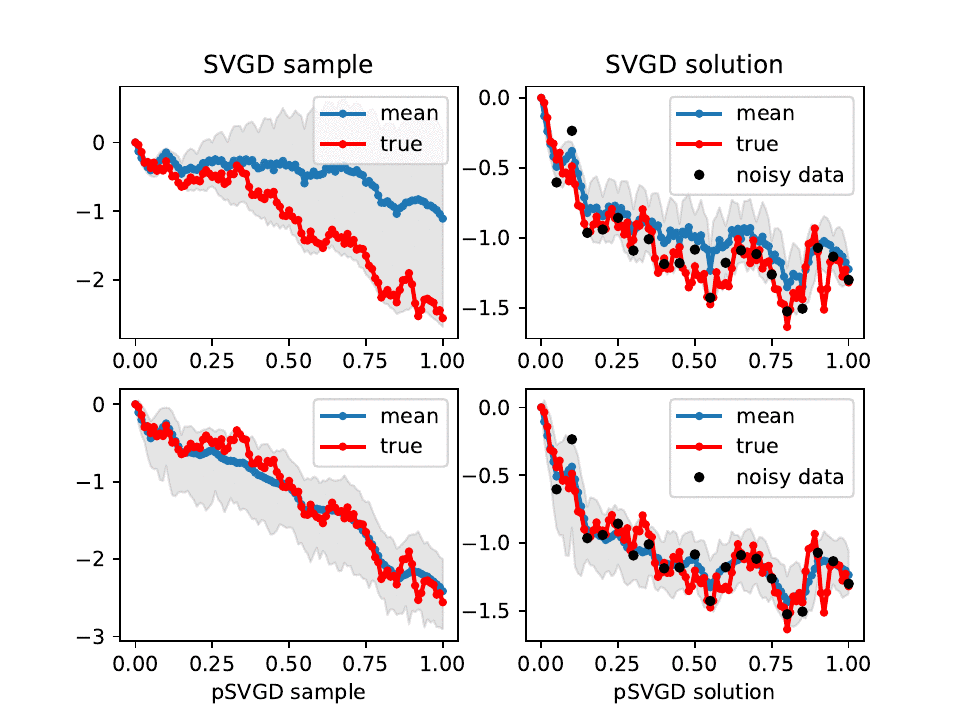
Evolution of SVGD (top) and pSVGD (bottom) parameter samples and their corresponding solutions of a conditional-diffusion model at iteration l = 0, 10, ..., 100. Shown are the true, sample mean, 90% credible interval, and noisy data.
By exploiting the intrinsic low-dimensional geometric structure of the posterior distributions in high-dimensional Bayesian inverse problems, we developed projected variational inference methods (pSVGD and pSVN) to tackle the curse of dimensionality faced in such problems. The methods are demonstrated to be fast, accurate, and scalable with respect to the number of parameters, samples, data points, and parallel processor cores for scientific, engineering, and machine learning problems.
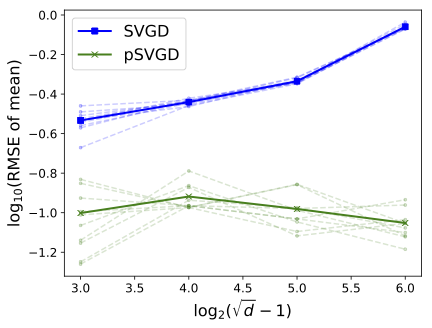
pSVGD preserves sample accuracy in increasing parameter dimension d (left)
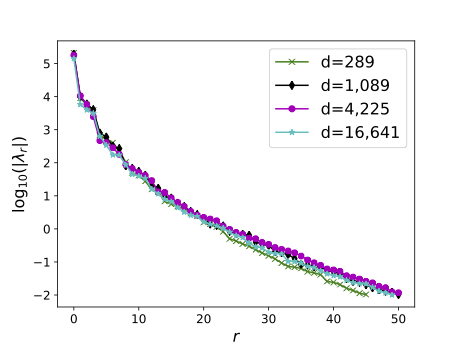
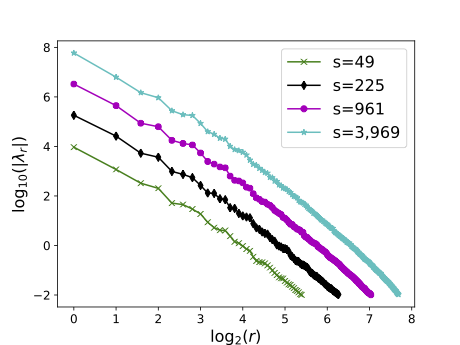
by exploiting the intrinsic low-dimensionality r detected by eigenvalues (right).
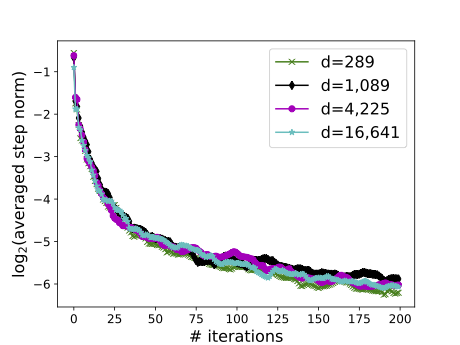
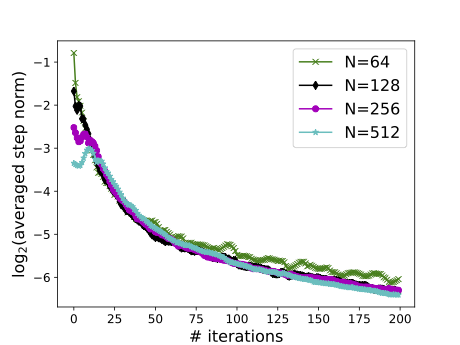
Complexity scalable with respect to # parameters (left) and samples (right).
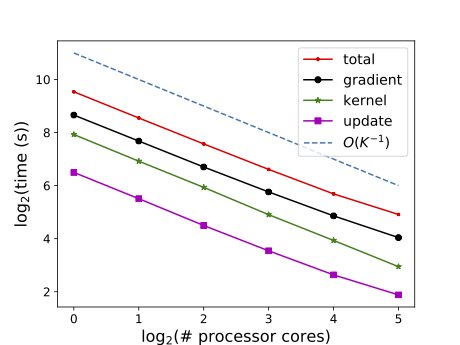
Weak scalable in # data (left) and strong scalable in # processor cores (right).
Reduced order model (ROM) is an important class of surrogates for high fidelity or full order model (FOM) that enables many-query statistical learning and stochastic optimization, real-time predictive simulation and system control. It compresses FOM with certified and computable error bound while preserving the model structure. We have contributed to the advancement of ROM by exploiting the structures of different models, probability distributions, and computational goals, and have developed weighted, goal-oriented, localized, adaptive, and learning algorithms in the applications of uncertainty quantification, reliability/failure probability analysis, model-constrained Bayesian inverse problems, optimal control, optimal experimental design, etc. Below is an illustration of FOM vs ROM, with a more detailed demonstration of ROM in Bayesian inversion.
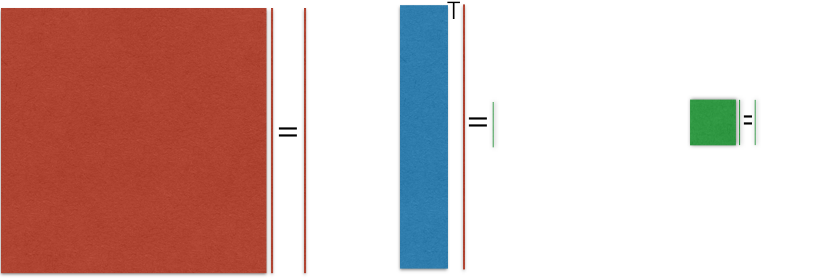
Compress large full order model (FOM) to small reduced order model (ROM).


Different representations for the same image, pixels (left) and SVD modes (right), have different dimensions (N2 vs N) and different preserved information.
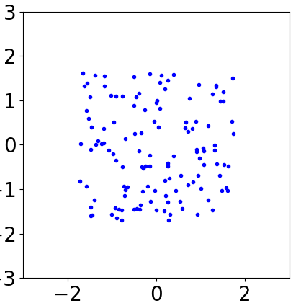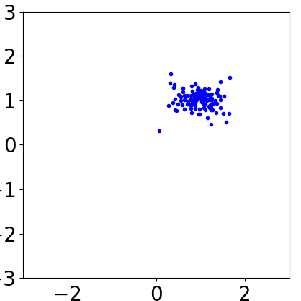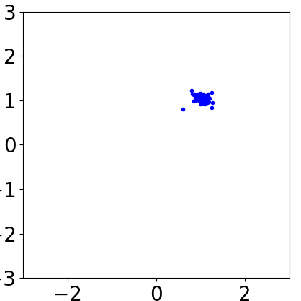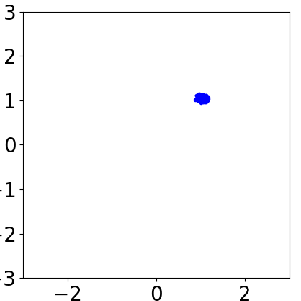
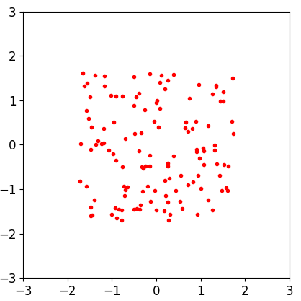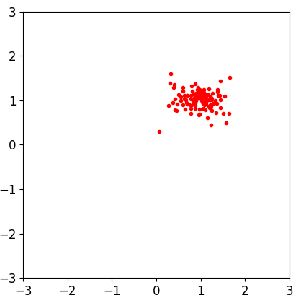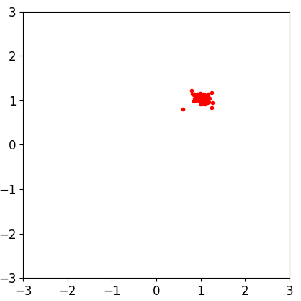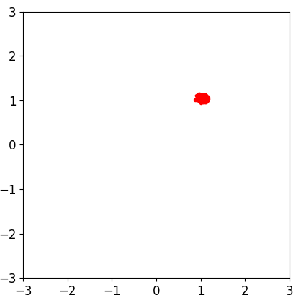
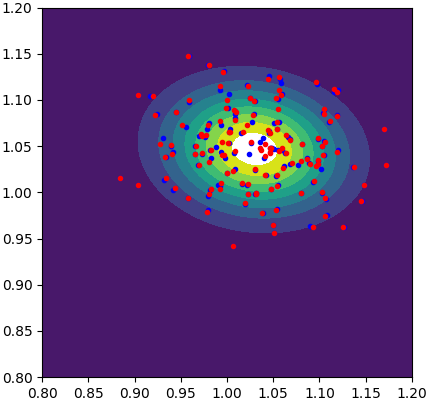
Sample evolution by FOM (left) and ROM (middle) to local posterior (right), which enables localized ROM construction, more efficient and accurate than global ROM.
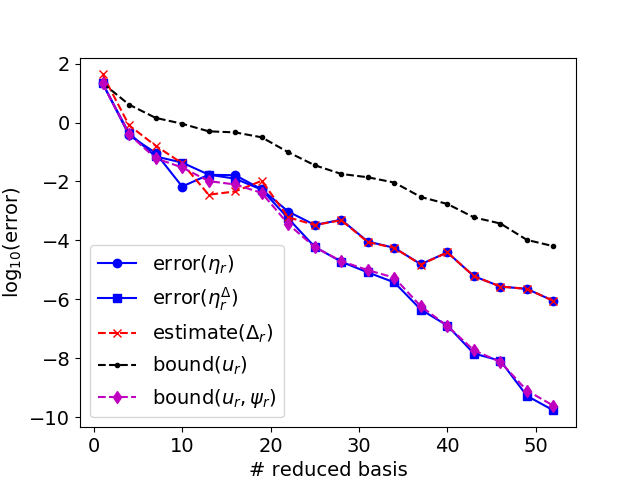
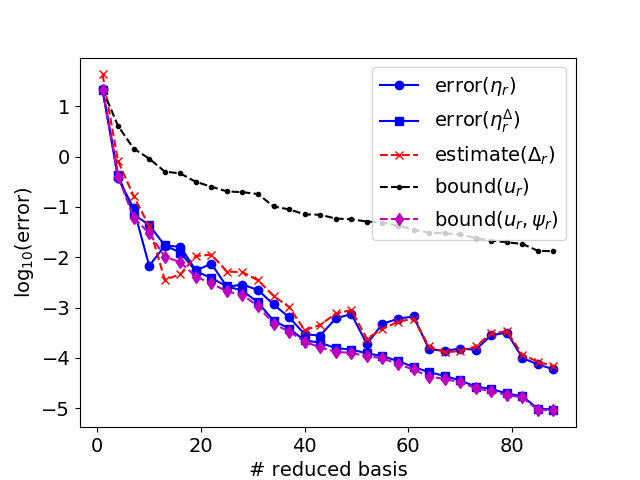
Convergence of ROM error and bounds for log-likelihood function w/ and w/o goal-oriented approximation by adaptive (left) and fixed (right) construction of ROM.
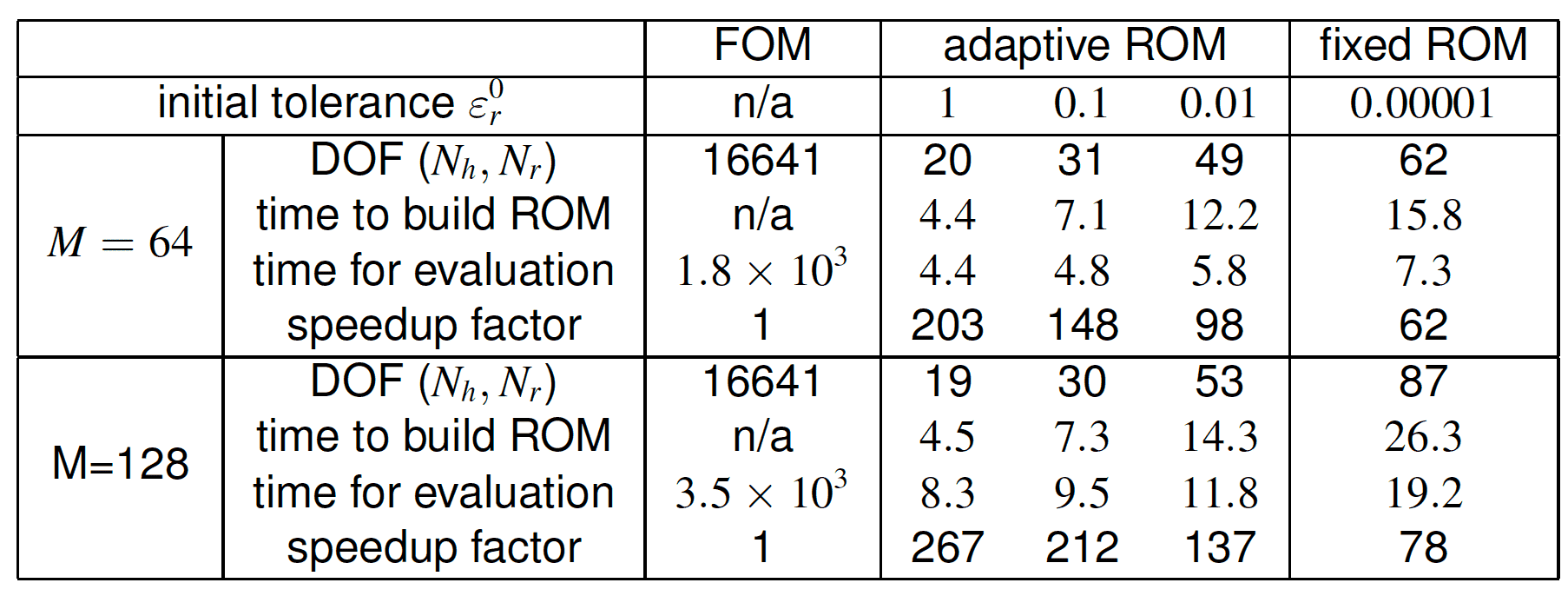
Computational speedup by adaptive and fixed construction of ROM with different tolerances and FOM for different number of Stein samples M.
In scientific machine learning governed by complex differential or integral equations, one often needs to learn operators that map input functions to output functions, both infinite or high-dimensional, with limited/small (expensive) training data. We developed projected neural networks that project the input and output functions into derivative-informed low-dimensional active subspaces and train a parsimonious neural network that is independent of the nominal dimensions and achieve high generalization accuracy with limited training data augmented with derivative information.
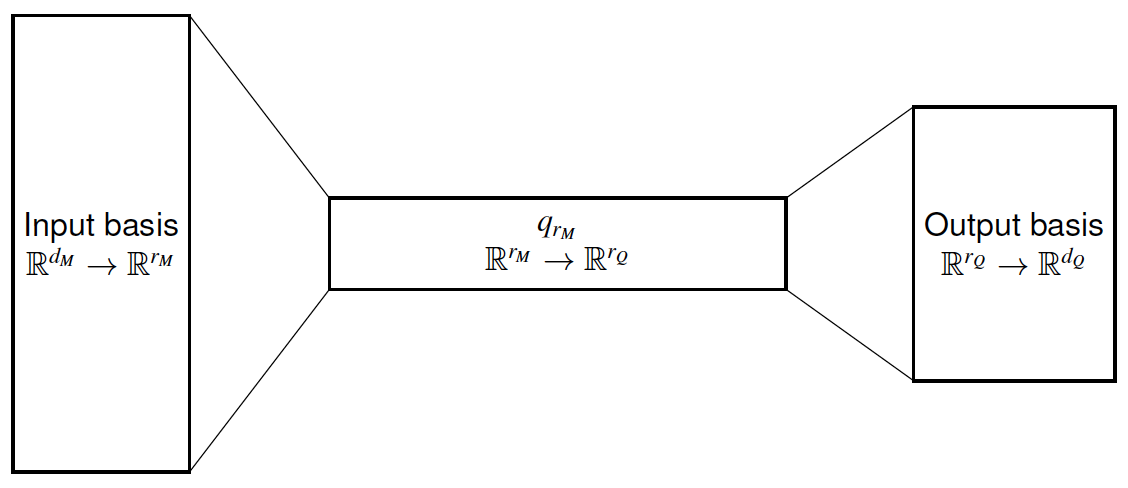
DIPNet with projection bases for high-dimensional input and output functions, computed by active subspace (AS) and proper orthogonal decomposition (POD).


Basis of active subspace (AS) vs Karhunen–Loève expansion (KLE).
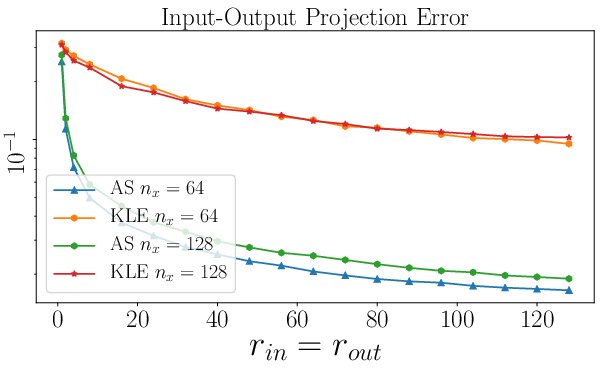
Basis by active subspace (AS) and Karhunen–Loève expansion (KLE).
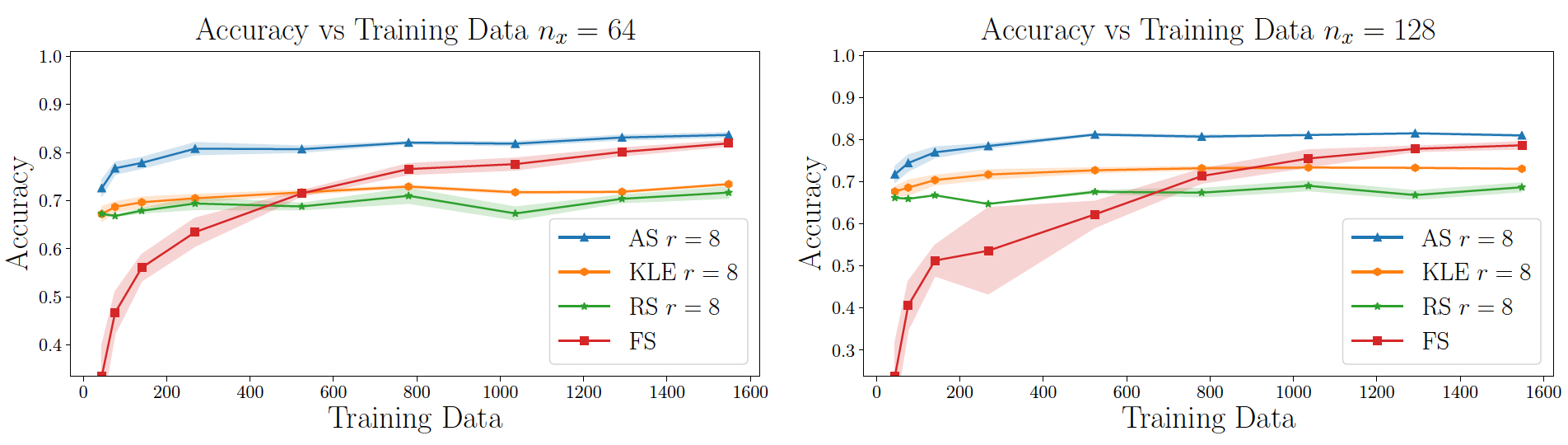
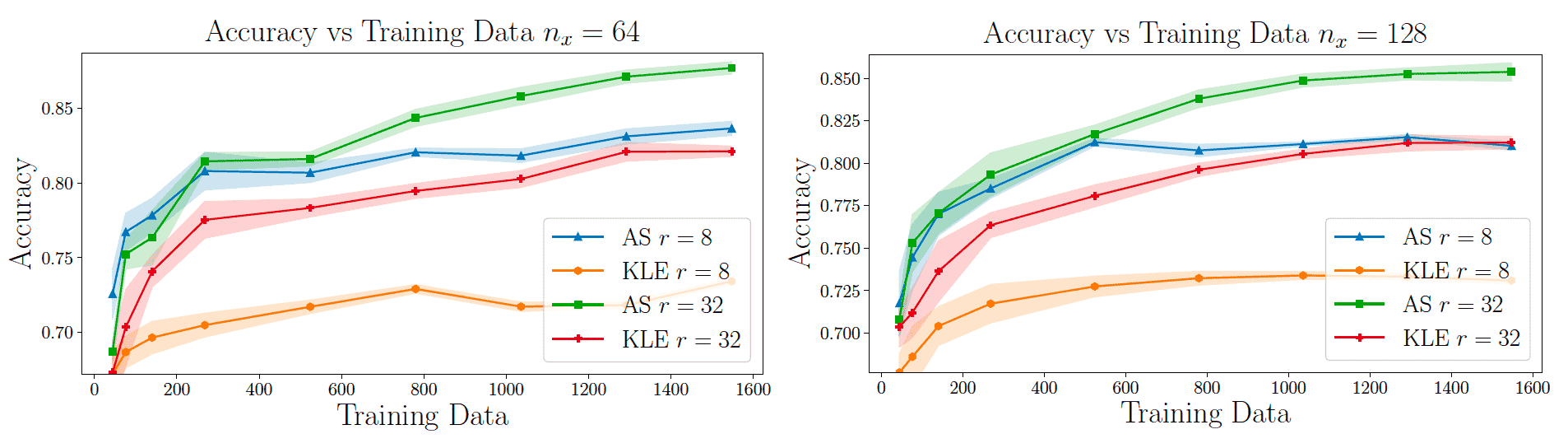
DIPNet using AS achieves higher generalization accuracy than that using KLE, random subspace (RS), and full space (FS) neural network for Helmholtz equation.

DIPNet has a fixed small 2,024 degrees of freedom (DOF) compared to the much higher DOF by full space neural network with different input dimensions.
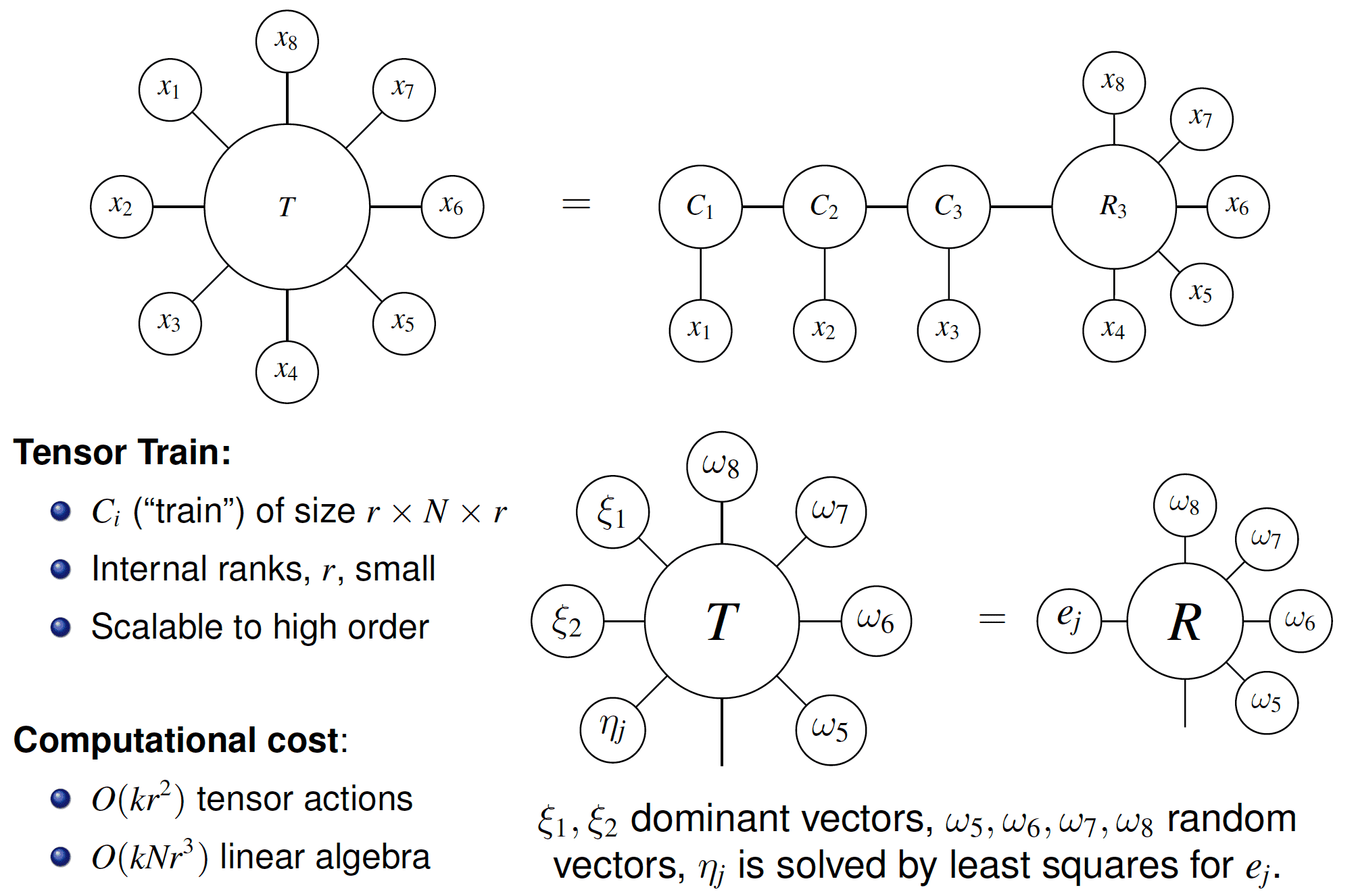
Construction of tensor train decomposition by peeling and randomized algorithms.
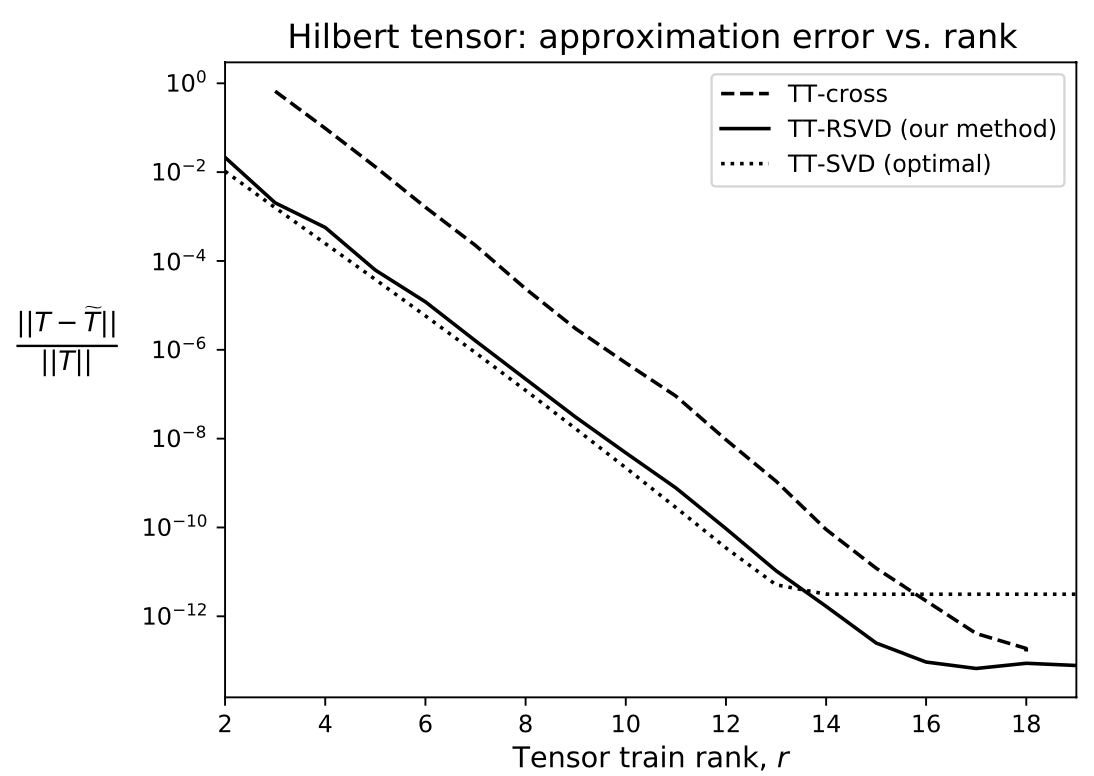
Comparison of tensor train decomposition methods for a 5th order Hilbert tensor.
We developed a scalable randomized algorithm for converting tensors into tensor train format based on actions of the tensor as a multilinear map. Existing methods for constructing tensor trains require access to the entries of the tensor and are therefore inefficient or computationally prohibitive if the tensor is accessible only through its action, especially for high-order (derivative) tensors. Our method allows efficient tensor train compression of large high-order derivative tensors for nonlinear mappings that are implicitly defined through the solution of a system of equations.
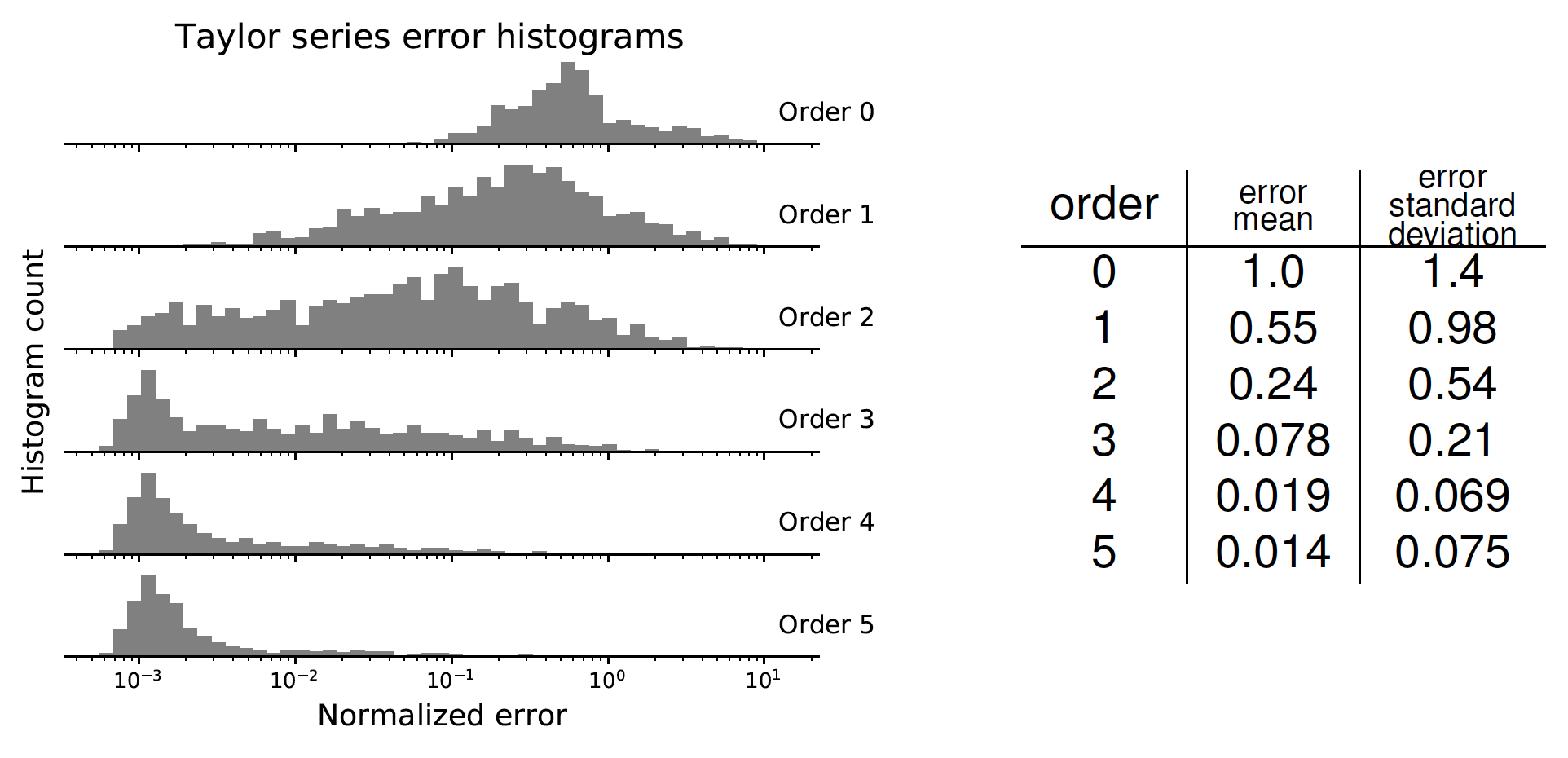
Convergence of functional Taylor approximation by tensor decomposition.
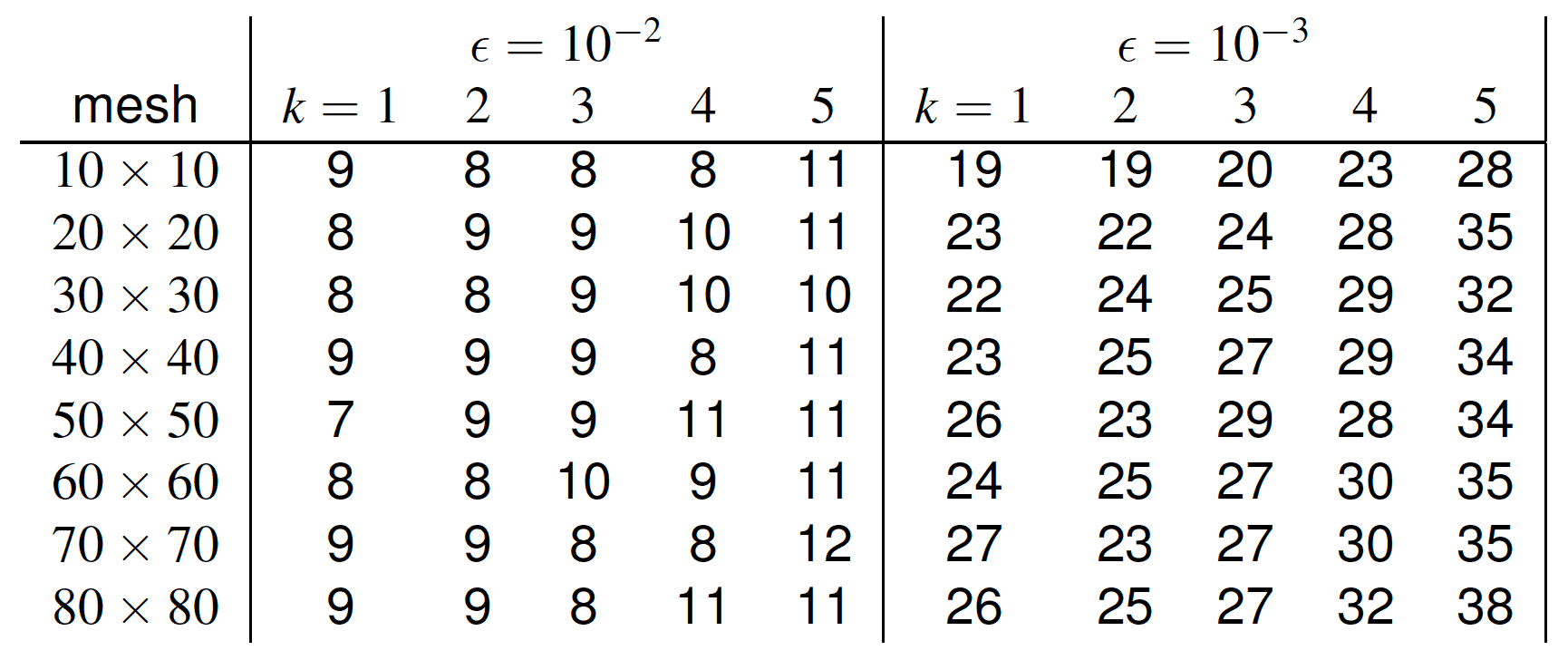
Complexity by tensor train rank is scalable in tensor size (mesh) and order (k).
We develop fast, scalable, and efficient methods for infinite-dimensional Bayesian OED problems using conditional normalizing flow and derivative-informed latent attention neural operators, achieving speedup of 100X - 1000X, accounting for both offline construction cost and online evaluation cost.
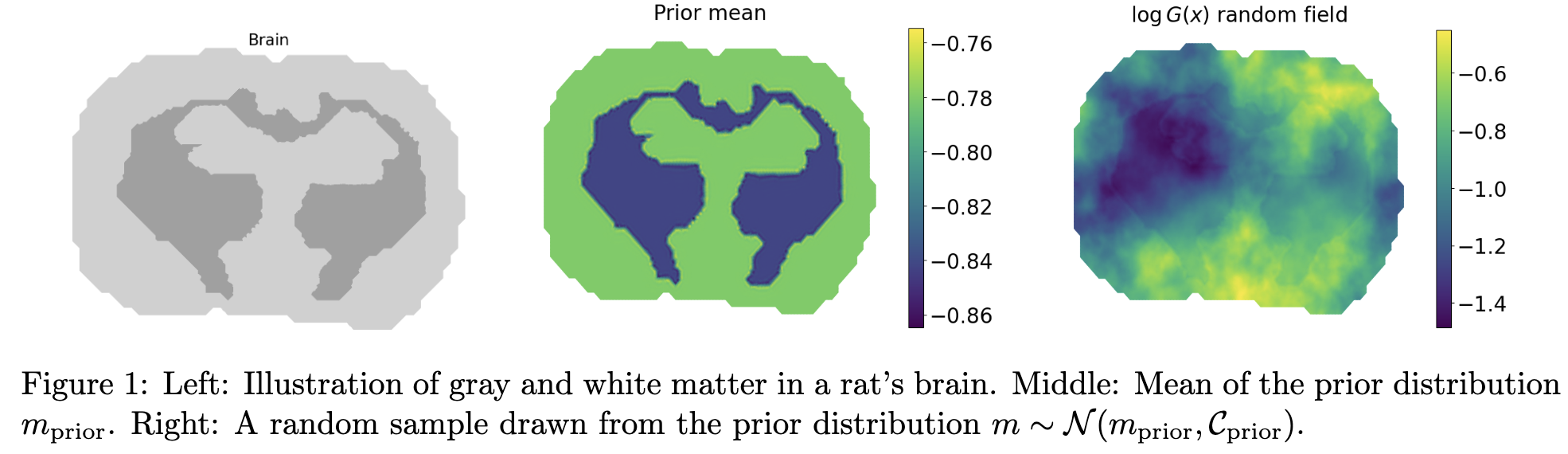
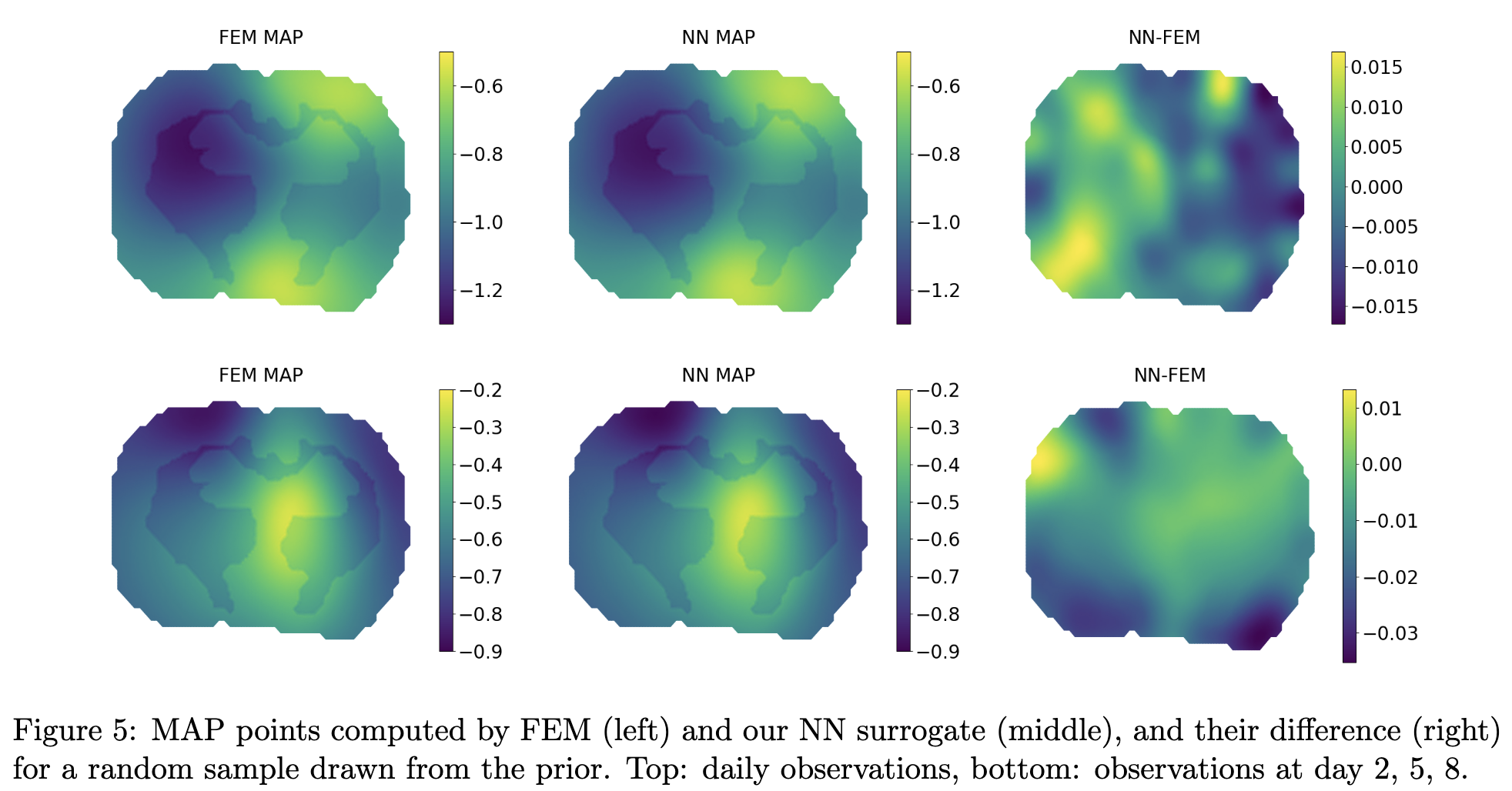
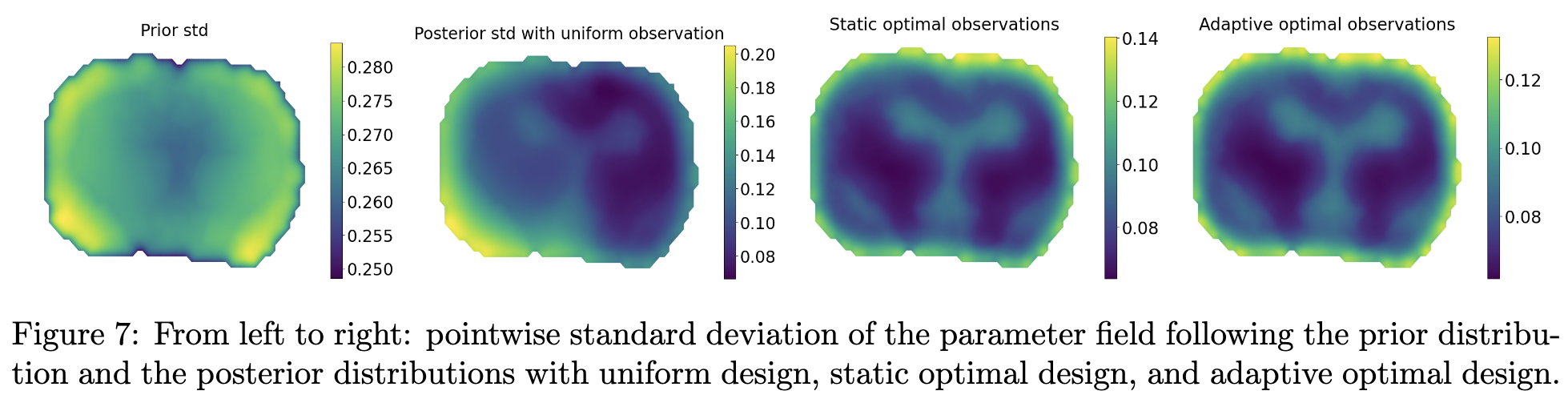

We developed a Taylor approximation-based approximate Newton method for stochastic optimal design of metamaterial cloak to hide obstacles (both an exemplary disk and a more complex geometry), under attack of manufacturing error of the metamaterials, multiple angles and frequencies of incident waves. The algorithm is demonstrated to be scalable (in terms of the number of PDE solves) with respect to both the uncertain parameter dimension (up to half a million) and the optimization variable dimension (over one million).
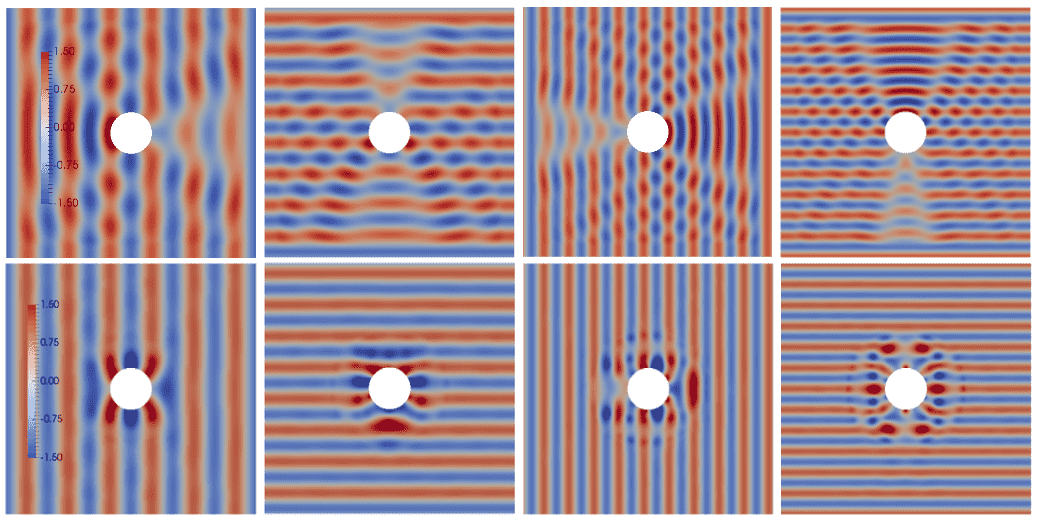
Total wave without (top) and with (bottom) metamaterial cloak around an obstacle, under attack of manufacturing errors, incident waves from multiple angles and frequencies.
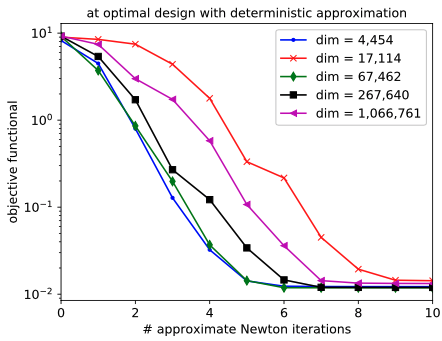
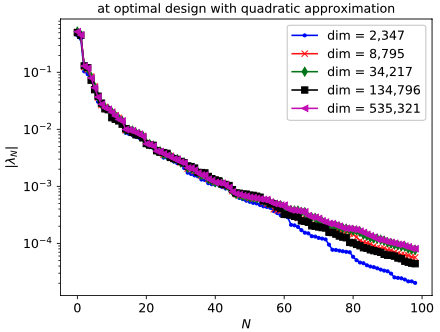
Convergence of the approximate Newton method (left) and eigenvalues of the Hessian of a parameter-to-output map that represent the intrinsic parameter dimensions.
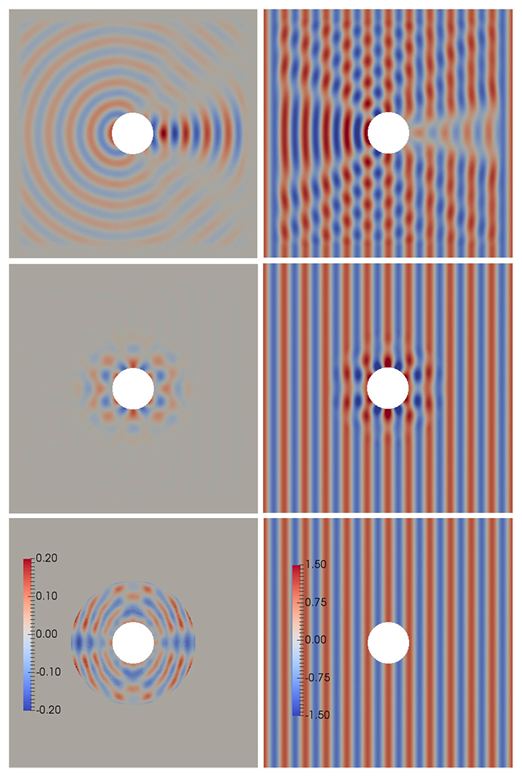
Top: scattered wave (left) and total wave (right) around an impenetrable obstacle. Middle: scattered wave (left) and total wave (right) with optimal metamaterial present around the obstacle. The scattered wave is eliminated by the metamaterial. Bottom: optimal design (left) and incident wave (right).
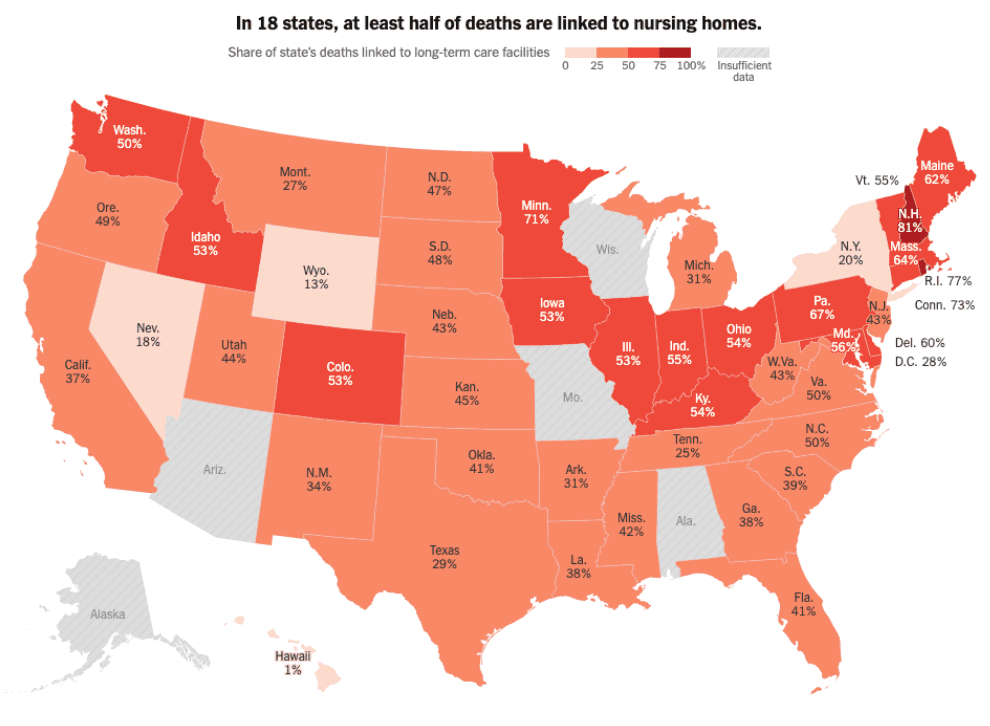
Share of COVID-19 deaths linked to long-term care facilities in US.
Source: The New York Times, September 16, 2020.
In the observation of overwhelming share of COVID-19 deaths from long-term care (LTC) facilities, we developed a data-driven decision making framework consisting a LTC-stratified SEIRHD compartment model, Bayesian inference of the model parameters (about 1500 dimensions) using our pSVGD method, and stochastic optimization of mitigation policy under parameter and operation uncertainties to reduce deaths and mitigation burden subject to chance constraint of hospital capacity.
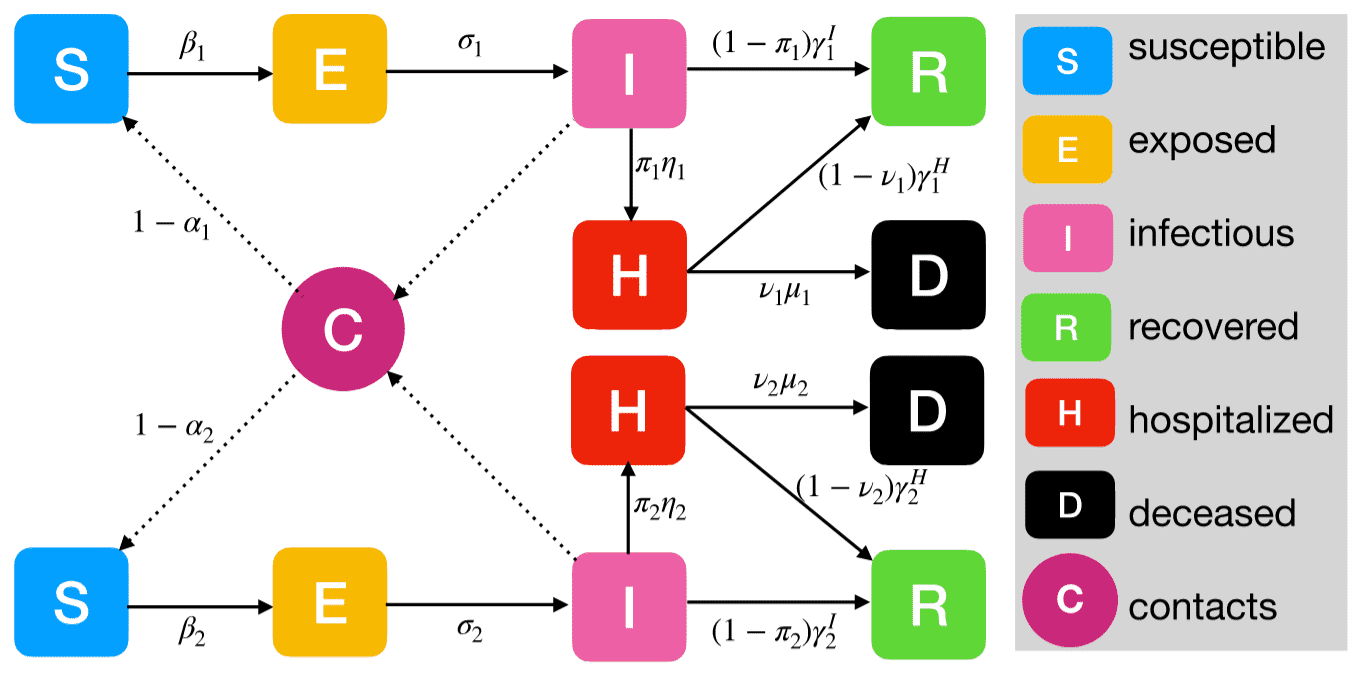
Diagram of a compartment model for COVID-19 inside (top part) and outside (bottom part) long-term care facilities with contacts of residents, staffs, and visitors.
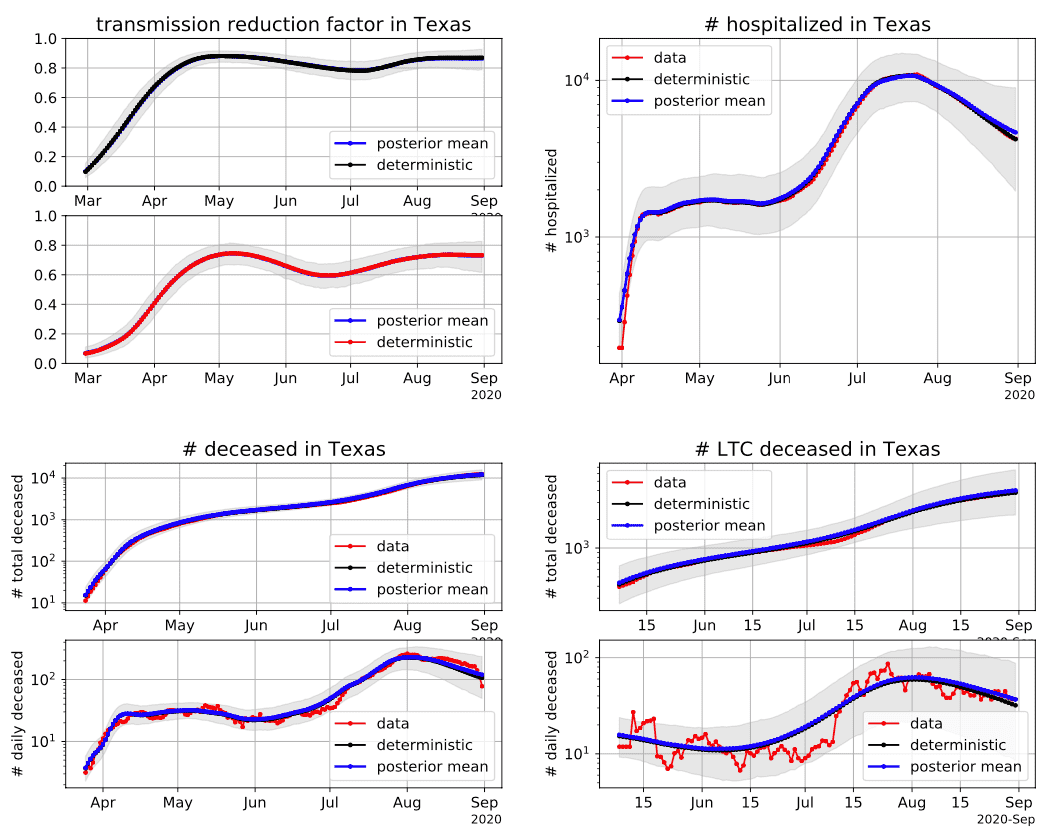
Data-driven model selection and learning by both deterministic and Bayesian inferences. Learned transmission reduction factor as a stochastic process among many other parameters (top-left), with quantified uncertainty in and out of LTC.
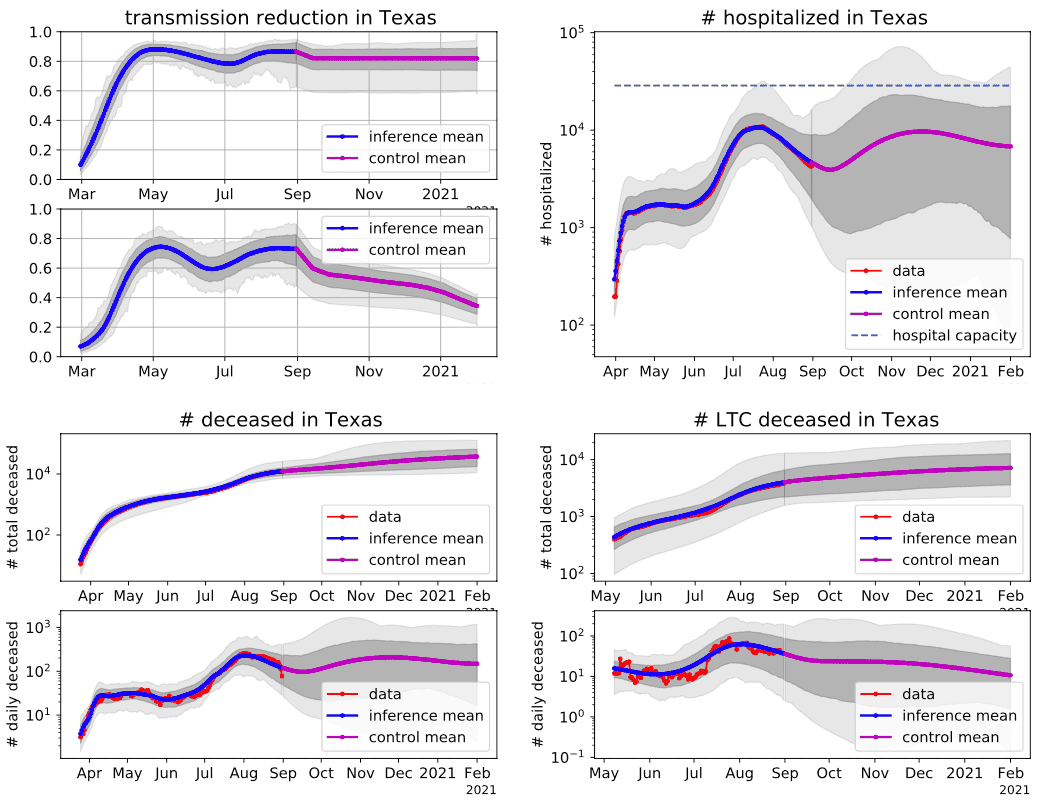
Predictive simulation-based stochastic optimal control of mitigation policy under parameter and operation uncertainties to reduce COVID-19 deaths and mitigation burden subject to chance/probability constraint of hospital capacity.
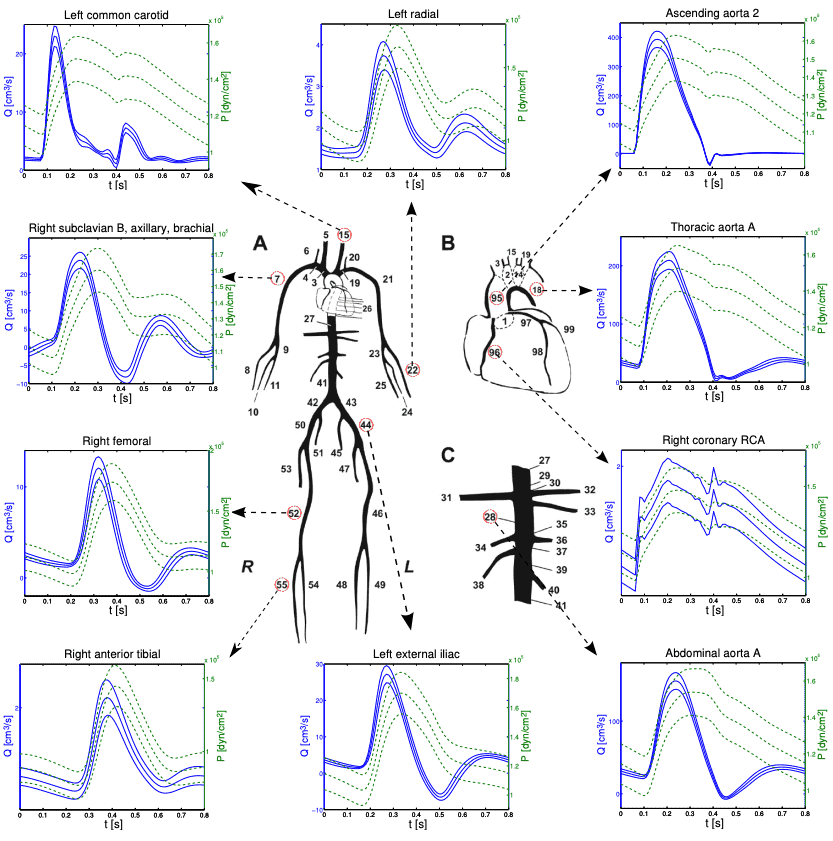
Uncertainty quantification of human arterial network hemodynamics (blood flow rate in blue and pressure in green) with respect to different physiological parameters using a fluid structure interaction model in each network segment.
We conducted uncertainty quantification and global sensitivity analysis of human arterial networks with 150 physiological parameters. The results help for better understanding of the influence of different physiological abnormalities to various cardiovascular diseases such as heart attack, stroke, aneurysms, aorta stiffening.
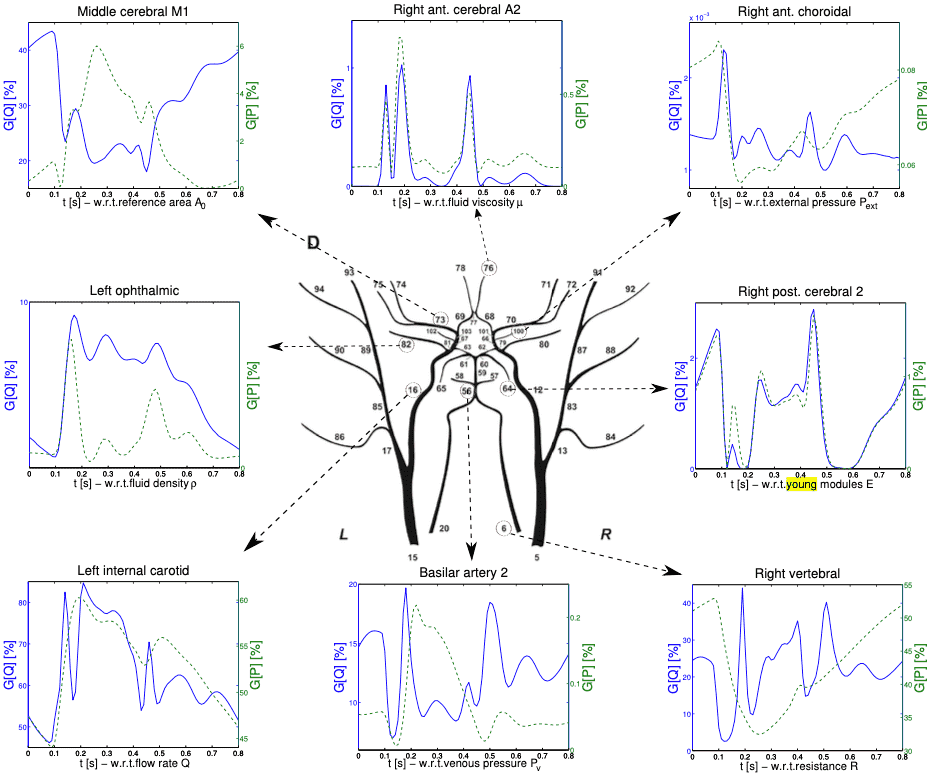
Global sensitivity analysis (using high-dimensional sparse grid quadrature) with respect to different physiological parameters in human cerebral arterial network.
We are working in Simons Collaboration on stochastic optimization for the design of the shape of stellarator devices, which facilitate magnetic confinement of plasma fusion in order to harness nuclear fusion power. One important concept--quasisymmetry--is critical to sustain stable plasma fusion. We are working on stochastic optimization of the quasisymmetry subject to manufacturing errors (which led to the termination of the NCSX construction) and operation uncertainties, employing automatic differentiation and parallel GPU computing.
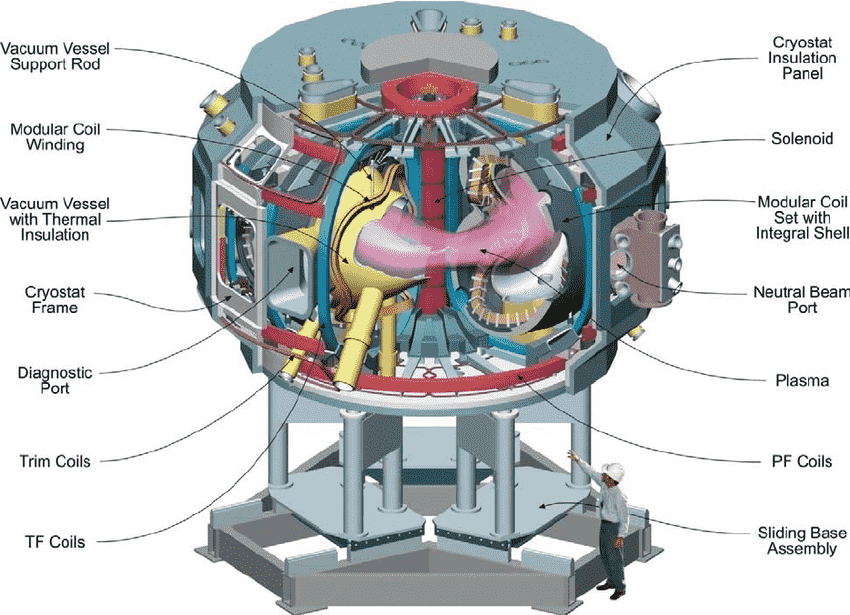
National Compact Stellarator Experiment (NCSX), a magnetic fusion energy experiment by stellarator design. The construction was terminated for manufacturing challenges, which we tackle by stochastic optimization.

Magnetic field as the solution of an ideal Magnetohydrodynamics (MHD) equation.

GPU-accelerated parallel stochastic optimization using HPC system Frontera.
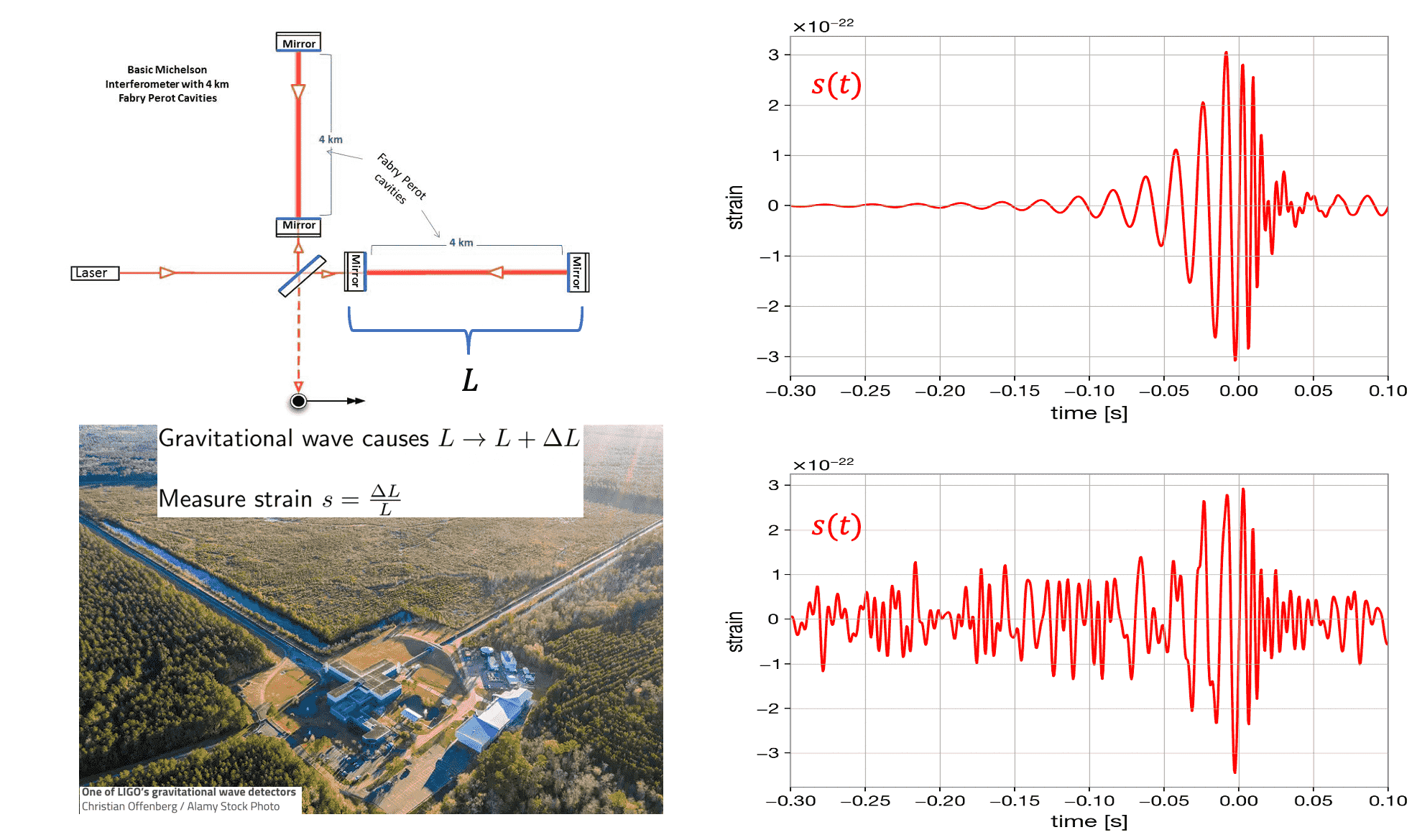
Gravitational wave detected by interferometer data as the strain measured by the phase change of recombined laser beams after bouncing back from mirrors.
Right: incredibly small synthetic strain w/ and w/o characteristic noise.
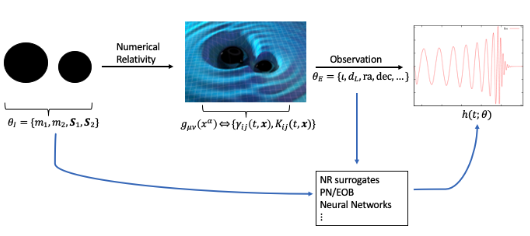
Multifidelity models for parameter-to-observable map, e.g., post-Newtonian (PN), perturbative effective-one-body (EOB), numerical relativity (NR) that solves Einstein's equations around a binary black hole system for gravitational wave.
Observational astronomy and gravitational-wave science entered into a new era after the first direct detection of gravitational waves by LIGO in September 14, 2015, as predicted by Einstein’s General Theory of Relativity. In collaboration with astrophysicists we are working on developing fast multifidelity Bayesian inference methods to learn parameters characterizing compact binary astronomical systems (such as black holes), which are enabled by a rich hierarchy of surrogates of the numerical relativity that solves Einstein field equations.
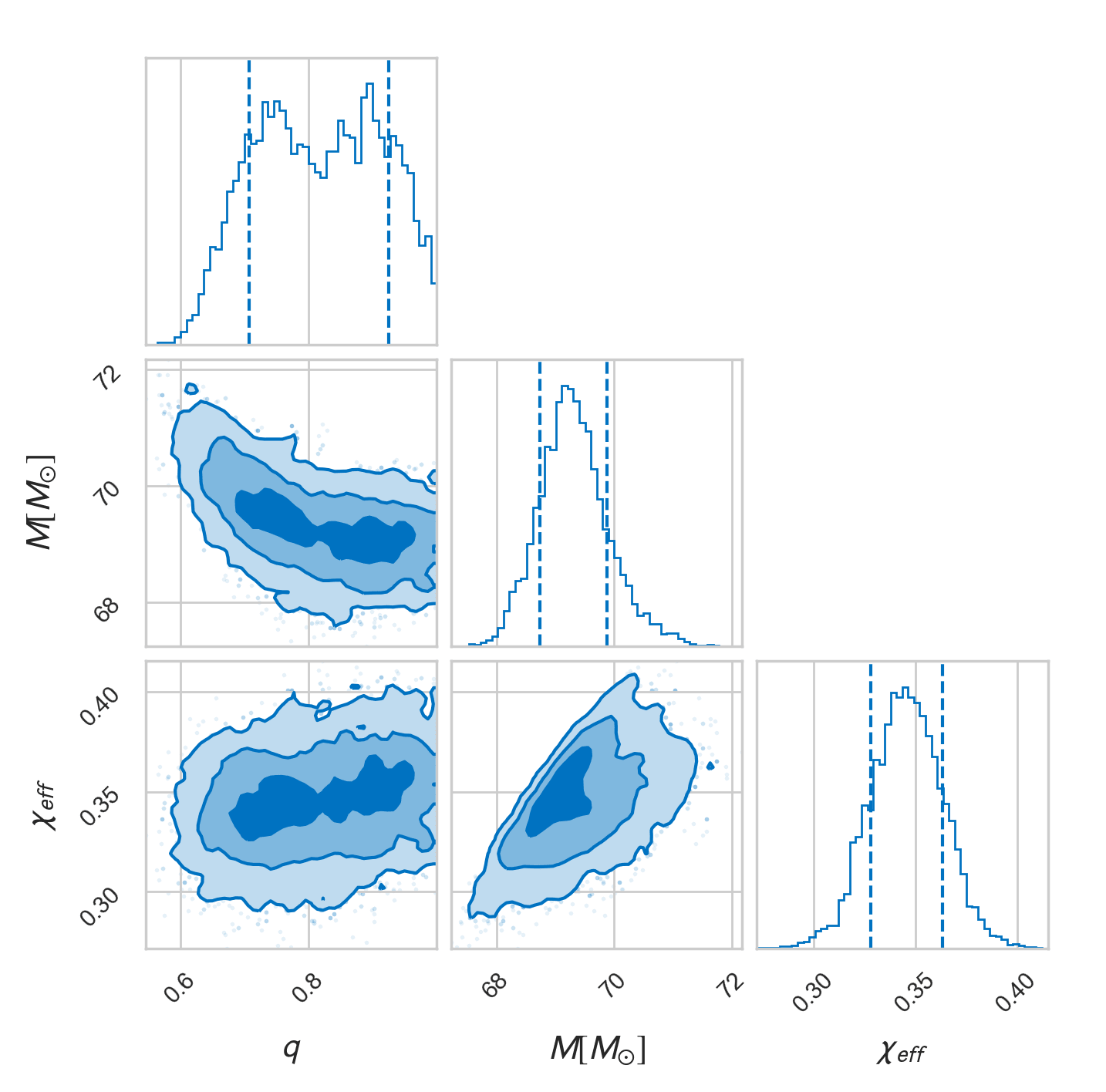
Marginal posterior densities of the most relevant intrinsic parameters:
mass ratio q=m1/m2, total mass M=m1+m2, effective spin magnitude χeff.