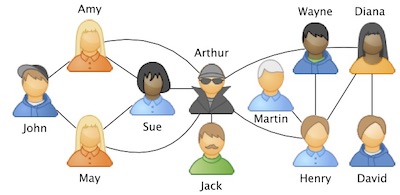
The betweenness and closeness metrics are widely used metrics in many
network analysis applications. Yet, they are expensive to compute. For that reason,
making the betweenness and closeness centrality
computations faster is an important and well-studied problem.
Closeness centrality is defined as:
\[far(u) = \sum_{v \in V, d(u,v)} d(u,v) \ \ \ \
cc[u] = \frac{1}{far(u)}\]
Betweenness centrality is defined as:
\[bc(u) = \sum_{s\neq u \neq t \in V} \frac{\sigma_{st}(u)}{\sigma_{st}}\]
We developed efficient parallel algorithms and vectorization techniques for
centrality computations. We proposed also proposed BADIOS framework which
manipulates the graph by compressing it and splitting into pieces so that the
centrality computation can be handled independently for each piece.
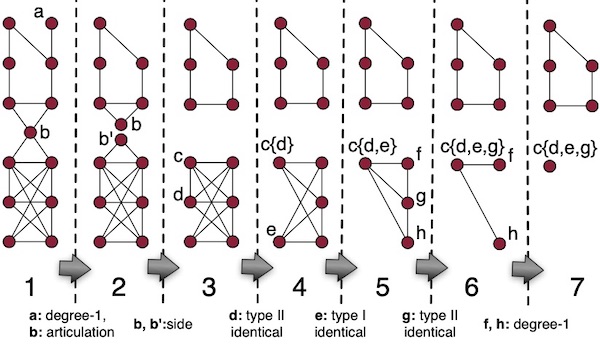
A sample iteration of BADIOS framework.
Related Publications
Graph Manipulations for Fast Centrality Computation
ACM Transactions on Knowledge Discovery from Data,
2017.
Incremental Closeness Centrality in Distributed Memory
Parallel Computing,
2015.
Regularizing Graph Centrality Computations
Journal of Parallel and Distributed Computing,
2015.
Computing the Closeness Centrality of Evolving Networks on Clusters
Poster, SIAM Workshop on Network Science (NS14),
2014.
Hardware/Software Vectorization for Closeness Centrality on Multi-/Many-Core Architectures
In 28th International Parallel and Distributed Processing Symposium Workshops, Workshop on Multithreaded Architectures and Applications (MTAAP),
2014.
Incremental Algorithms for Closeness Centrality
In Proc of IEEE Int’l Conference on BigData,
2013.
STREAMER: a Distributed Framework for Incremental Closeness Centrality Computation
In Proc. of IEEE Cluster 2013,
2013.
Shattering and Compressing Networks for Betweenness centrality
In SIAM International Conference on Data Mining (SDM),
2013, An extended version is available on ArXiv.
Betweenness Centrality on GPUs and Heterogeneous Architectures
In Workshop on General Purpose Processing Using GPUs (GPGPU), in conjunction with ASPLOS,
2013.
Incremental Algorithms for Network Management and Analysis based on Closeness Centrality
ArXiv arXiv:1303.0422,
2013.
Shattering and Compressing Networks for Centrality Analysis
ArXiv arXiv:1209.6007,
2012.