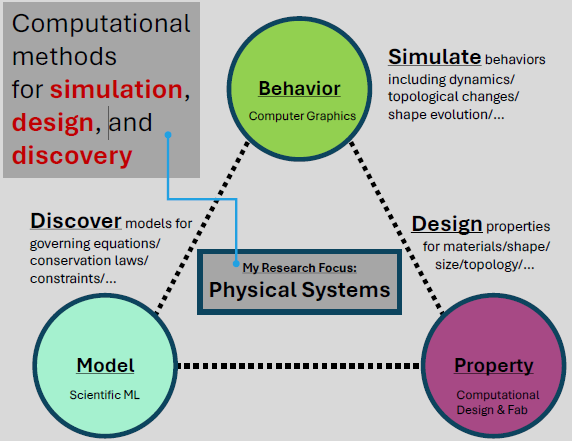
My group's research focuses on three interrelated areas: physics-based simulation, physics-embedded machine learning, and computational design. These thrusts connect core disciplines across computer graphics, computational physics, scientific machine learning, and computational fabrication. As illustrated in the image, they jointly address the multifaceted challenges of understanding and exploring complex physical systems through their behavior, models, and properties.

1. Physics-Based Simulation: We develop first-principle simulation algorithms to model the complex behavior of physical systems, focusing on their dynamics, geometry, and topology. We particularly focus on devising geometric representations and numerical methods for simulating fluid systems relevant to graphics, science, and health applications.

2. Physics-Embedded Machine Learning: We develop scientific machine learning algorithms to uncover hidden models from data and support robust long-term predictions. Our approach focuses on prior-embedded network architectures and simulation-adapted neural representations to address complex physical systems where traditional models are insufficient or unavailable.

3. Computational Design: We devise computational methods to automate the design and exploration of complex physical systems. We aim to build fully automated pipelines that probe property boundaries and performance limits of systems coupling structure, material, and control.

Physics-based Simulation

My group investigates computational methods for simulating fluid systems featured by complex interfacial dynamics and vortical evolution. A particular focus is placed on small-scale fluid systems such as thin sheets, filaments, bubbles, foams, droplets, and aerosols, along with their interactions with vortical structures, which exhibit intricate multiscale and multiphysics behavior. These fluid structures play critical roles in biological and physiological systems and also represent visually complex phenomena of significant interest to the computer graphics community. To address these simulation challenges, we develop geometric representations that combine continuous mathematical formulations with discrete data structures to model dynamic processes involving complex geometry and topology. On the modeling side, we introduce new gauge formulations of the Navier-Stokes equations—including impulse-based and Clebsch-based models—to simulate incompressible flows with strong vortical and interfacial features. On the numerical side, we construct Lagrangian discretizations ranging from mesh-based representations to particle systems and spacetime flow maps. Our representation pipeline has progressed from simplicial and embedded meshes to moving particles, and most recently to unified flow-map-based schemes for tracking spacetime evolution.

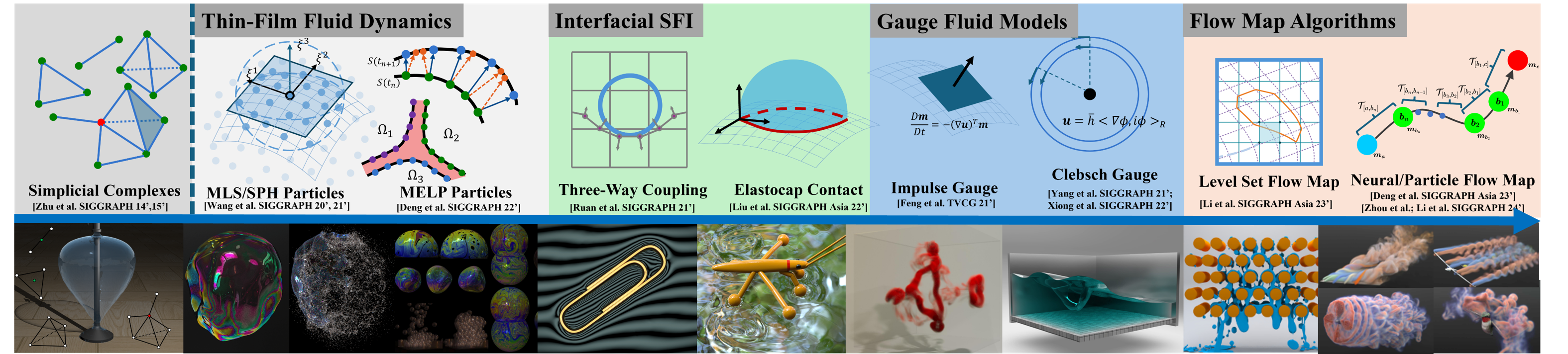
These advances have enabled the simulation of a broad class of small-scale fluid phenomena that were previously inaccessible. Notable examples include cherries floating on water, soap bubble bursting and foam dynamics, horseshoe vortices generated by locomotion, and capillary interactions between droplets and solids. These simulations have helped visualize and analyze fluid processes underlying biological locomotion, respiratory droplet transmission, and fluid-surface interactions, and have supported interdisciplinary collaborations in graphics, physics, and bioengineering.

Representative Works:

• Thin-Film Fluid Dynamics: We developed simulation algorithms for thin films that accurately model the visual and physical evolution of soap bubbles and foam clusters, capturing separation, coalescence, color interference, and vortex transport.
• Interfacial Solid-Fluid Interaction: Our models simulate capillary-driven solid-fluid contact, enabling high-fidelity elastocapillary simulations such as droplets on hydrophobic surfaces and deformable solids interacting with thin films.
• Gauge Fluid Methods: We proposed novel gauge-based formulations—including impulse and Clebsch variables—for incompressible flow, improving the long-range preservation of vorticity and interfacial structure in fluid systems.
• Flow Map Algorithms: We introduced particle-based flow map methods for simulating incompressible flow. These algorithms capture the transport of point-, line-, and area-based features and support robust modeling of interfaces and vortical structures across time.

Physics-Embedded Machine Learning

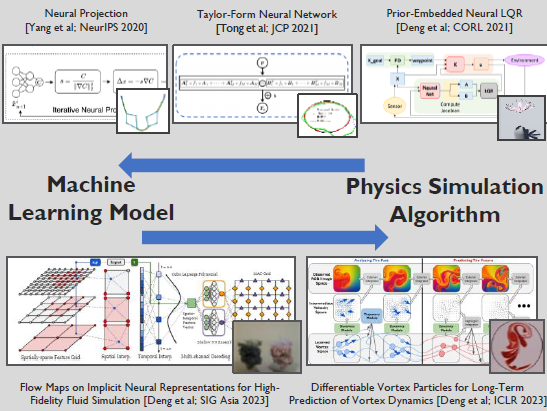
We develop machine learning methods that are tightly coupled with physical modeling principles to address simulation and inference tasks that are difficult to solve using purely first-principle approaches. Our research focuses on embedding physical priors into the structure of neural networks and simulation frameworks to enhance data efficiency, generalization, and physical consistency. One direction of our work focuses on embedding mathematical and physical constraints into neural architectures. We design novel network modules, time integration schemes, and PDE-inspired layers to decouple a model’s expressiveness from data scale and connectivity. These prior-embedded architectures have enabled the long-term prediction of Hamiltonian and transport systems under limited supervision, by explicitly preserving geometric or symplectic properties of the dynamics. In parallel, we also develop data-driven simulation algorithms that incorporate differentiable geometric discretizations, lightweight neural surrogates, and implicit representations to improve the efficiency and fidelity of physical simulation pipelines. This includes our recent work on neural flow maps, where high-dimensional latent spaces are used to encode complex, long-term fluid dynamics, allowing accurate simulations in settings where conventional solvers are inefficient or unstable.

Representative Works:

• Prior-Embedded Neural Networks: We designed structure-preserving neural models that incorporate symplectic and sparsity constraints to enable stable long-horizon predictions in Hamiltonian systems under sparse data conditions.
• Simulation with Neural Representations: We developed simulation frameworks using high-dimensional neural fields and flow maps that support differentiable and physically faithful evolution across space and time.

Computational Design and Fabrication

Our group develops computational methods to automate the design and exploration of complex physical systems. We focus on building optimization frameworks that integrate simulation-based models, data-driven representations, and interactive user interfaces, with the goal of reducing the complexity and cost of designing physical functionalities and embodied intelligence. The designs generated by our algorithms (see image) span a wide range of physical domains.

Our methodology is structured around two key components. First, we construct novel representations of the design space that enable efficient search over high-dimensional and nonconvex domains, overcoming traditional limitations such as the curse of dimensionality and the prevalence of poor local minima. For example, we introduced differentiable Voronoi diagram representations for topology optimization in thin-shell structures inspired by biological forms, such as dragonfly wings. Similarly, we have used continuous implicit representations for metamaterial design to explore microstructural properties such as stiffness, elastic modulus, and density. Second, we develop differentiable physics simulators that enable gradient-based optimization for complex physical systems where conventional methods are either unstable or inefficient. These simulators allow end-to-end coupling of physical simulation and design objectives, and have been applied to domains such as magnetic thin-shell robots, soft-bodied aerial drones, microfluidic circuits, and functional grippers. These tools provide a computational foundation for discovering novel designs across scales and applications.