Computer VisionMy group's research in computer vision has followed two main branches: the application of probabilistic models to the segmentation problem, and developing tracking methods that could be used as a front end for visual servo control. Our main contribution to the segmentation problem has been an approach in which multiple segmentation hypotheses can be explored within a Bayesian framework. The main idea is to implicitly characterize large sets of possible segmentations that have low probability, while explicitly computing probabilities for those segmentations that are more likely. We have applied the method to various parametric image models for range and intensity images, as well as to the problem of perceptual grouping. For the problem of tracking, we have used Kalman filtering methods to track articulated objects (e.g., robot arms). We have also developed an approach for estimating the covariance matrix (for the Kalman filter) directly from observed image data. We have also used critical point filter methods to define features for tracking using the qualitative structure of a multi-resolution image intensity map. In addition to these, we have worked on planning next best views, inspection algorithms that use subpixel methods, and segmentation of MRI images (work that was done in Paris, in the research group of Isabelle Bloch). An overview of the main projects is given below. Tracking
| |
| | |
Model-Based Tracking of Complex Articulated ObjectsKevin Nickels and Seth Hutchinson | |

|
In this work, we developed methods for tracking complex, articulated objects. We assume that an appearance model and the kinematic structure of the object to be tracked are given, leading to a model-based object tracker. At each time step, this tracker observes a new monocular grayscale image of the scene and combines information gathered from this image with knowledge of the previous configuration of the object to estimate the configuration of the object at the time the image was acquired. Each degree of freedom in the model has an uncertainty associated with it, indicating the confidence in the current estimate for that degree of freedom. These uncertainty estimates are updated after each observation. An extended Kalman filter with appropriate observation and system models is used to implement this updating process. |
| This work is described in Kevin's T-RO paper: Back to top | |
| | |
Real-Time Object Tracking using Multi-Resolution Critical Points FiltersJerome Durand, Brad Chambers and Seth Hutchinson | |
 |
|
|
In this work, we developed a real-time tracking system based on
feature points extracted by multiresolution critical-point filters (CPF).
The algorithm is able to revise these points at each iteration
to account for events that may have otherwise caused feature points to be lost,
leading to tracking failure.
A key advantage of the
method is that it is not affected by the movements (within a certain reasonable
range) of the camera or the object; such as, translation, rotation or scaling.
The algorithm is also insensitive to regular changes of the object's shape.
The figure above shows an original image, and the output of the four critical point filters at the fifth level of the resolution hierarchy. From left to right, they are: min(min,min), max(min,min), min(max,max), and max(max,max). | |
This work is described in two papers. An IROS paper
describes the features detection, and an ICRA paper describes
the tracking algorithm.
| |
| | |
Estimating Uncertainty in SSD-Based Feature TrackingKevin Nickels and Seth Hutchinson | |
|
Sum-of-squared-differences (SSD) based feature trackers
use SSD correlation measures to locate target features in sequences of images.
The results can then be used to estimate the motion of objects in the scene,
to infer the 3D structure of the scene, or to control robot motions.
The reliability of the information provided by these trackers can be degraded
by a variety of factors, including changes in illumination, poor image
contrast, occlusion of features, or unmodeled changes in objects. This has led
other researchers to develop confidence measures that are used to either accept
or reject individual features that are located by the tracker.
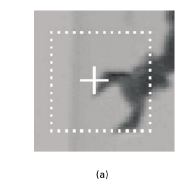
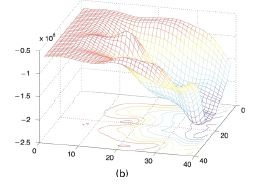
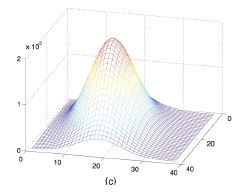
In this work, we derived quantitative measures for the spatial uncertainty of the results provided by SSD-based feature trackers. Unlike previous confidence measures that had been used only to accept or reject hypotheses, our measure allows the uncertainty associated with a feature to be used to weight its influence on the overall tracking process. Specifically, we scale the SSD correlation surface, fit a Gaussian distribution to this surface, and use this distribution to estimate values for the observation covariance matrix in an extended Kalman filter. The figure to the left shows (a) a target image with a dotted box showing the area search, with a cross superimposed on the feature location (b) negative SSD surface, (c) the Gaussian density that best fits the SSD surface, and which defines the covariance matrix for the EKF. This work is described in Kevin's Image and Vision Computing paper: |
| Back to top | |
| | |
A Bayesian Framework for Constructing Probability Distributions on the Space of Image SegmentationsSteve LaValle and Seth Hutchinson | |
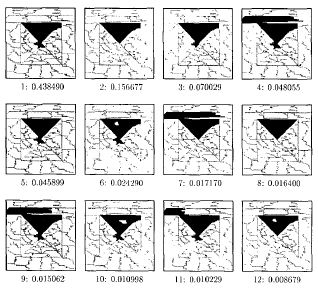
|
The goal of traditional probabilistic approaches to image segmentation has been
to derive a single, optimal segmentation, given statistical models for the
image formation process.
In this work, we developed a probabilistic approach to segmentation,
in which the goal is to derive a set of plausible segmentation hypotheses
and their corresponding probabilities.
Because the space of possible image segmentations is too large to represent explicitly, we
developed a representation scheme that allows the implicit representation of
large sets of segmentation hypotheses that have low probability. We then derived
a probabilistic mechanism for applying Bayesian, model-based evidence to guide
the construction of this representation. One key to our approach is a general
Bayesian method for determining the posterior probability that the union of
regions is homogeneous, given that the individual regions are homogeneous. This
method does not rely on estimation and properly treats the issues involved when
sample sets are small and estimation performance degrades.
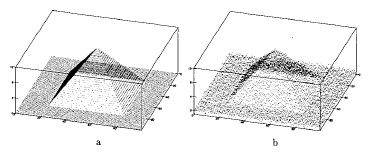
The figure to the left illustrates the probability distribution over a set of segmentation hypotheses for one surface of the tetrahedron. |
| This work is described in Steve's Computer Vision and Image Understanding paper: Back to top | |
| | |
A Bayesian segmentation methodology for parametric image modelsSteve LaValle and Seth Hutchinson | |

|
Region-based image segmentation methods require some criterion for determining
when to merge regions.
In this work,
we introduced a
Bayesian probability of homogeneity in a general statistical context. The
approach does not require parameter estimation and is therefore
particularly beneficial for cases in which estimation-based methods are most
prone to error: when little information is contained in some of the regions
and, therefore, parameter estimates are unreliable.
We applied our
formulation to three distinct parametric model families that have been used in
past segmentation schemes: implicit polynomial surfaces, parametric polynomial
surfaces, and Gaussian Markov random fields.
We have presented results on a
variety of real range and intensity images.
The figure to the left shows a variety of segmentation results obtained using the method. |
| This work is described in Steve's PAMI paper: Back to top | |
| | |
Textured Image Segmentation: Returning Multiple SolutionsKevin Nickels and Seth Hutchinson | |

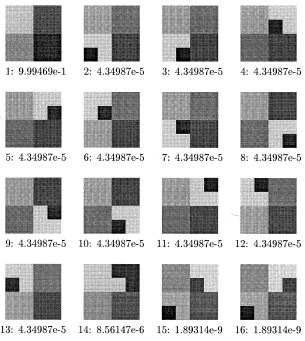
|
|
|
In this work,
we applied our multi-hypothesis segmentation method to intensity images
using texture models.
The probabilistic framework that enables
us to return a probability measure on each result also allows us to discard from
consideration entire classes of results due to their low cumulative
probability. The distributions thus returned may be passed to higher-level
algorithms to better enable them to interpret the segmentation results.
For this work,
we used Markov random fields as texture models
to generate distributions of segments and segmentations on textured images.
We tested our approach on
both simple homogeneous images and natural scenes.
The figure above shows an image comprised of four textures from the Brodatz texture database (left) and the sixteen most likely segmentations of the image, using a coarse pre-segmentation (right). | |
| This work is described in Kevin's Image and Vision Computing paper: Back to top | |
| | |
A Probabilistic Approach to Perceptual GroupingBecky Castano and Seth Hutchinson | |
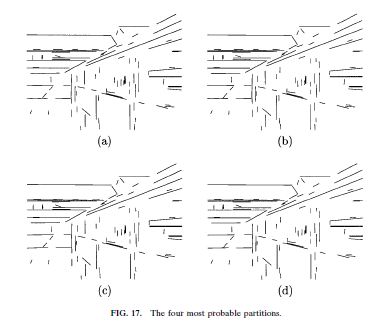
|
In this work, we extended our multi-hypothesis segmentation method to the problem of perceptual grouping. We derived a general framework for determining probability distributions over the space of possible image feature groupings. The framework can be used to find several of the most probable partitions of image features into groupings, rather than just returning a single partition of the features as do most feature grouping techniques. In addition to the groupings themselves, the probability of each partition is computed, providing information on the relative probability of multiple partitions that few grouping techniques offer. In determining the probability distribution of groupings, no parameters are estimated, thus eliminating problems that occur with small data sets and outliers such as the compounding of errors that can occur when parameters are estimated and the estimated parameters are used in the next grouping step. We have instantiated our framework for the two special cases of grouping line segments into straight lines and for grouping bilateral symmetries with parallel axes, where bilateral symmetries are formed by pairs of edges. Results were obtained for these cases on several real images. |
| This work is described in Becky's Computer Vision and Image Understanding paper: Back to top | |
| | |
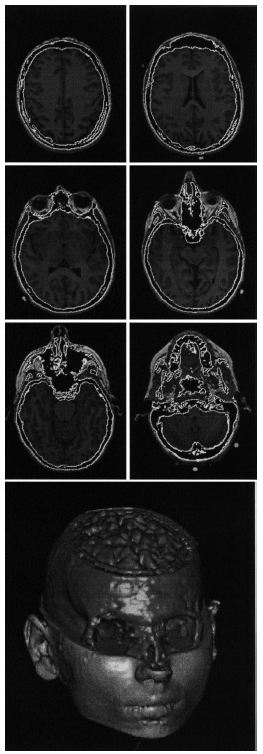
Segmentation of the Skull Using Deformable Model and Taking Partial Volume Effect into AccountH. Rifai, I. Bloch, J. Wiart, L. Garnero, and Seth Hutchinson | |
 |
This work was mainly done by Hilmi Rifai, at the ENST in Paris,
during the course of his PhD studies
with Isabelle Bloch.
I happened to be at the ENST at that time, on a sabbatical leave
from the University of Illinois.
Segmentation of the skull in medical imagery is an important stage in applications that require the construction of realistic models of the head. Such models are used, for example, to simulate the behavior of electro-magnetic fields in the head and to model the electrical activity of the cortex in EEG and MEG data. In this work, we developed a new approach for segmenting regions of bone in MRI volumes using deformable models. Our method takes into account the partial volume effects that occur with MRI data, thus permitting a precise segmentation of these bone regions. At each iteration of the propagation of the model, partial volume is estimated in a narrow band around the deformable model. Our segmentation method begins with a pre-segmentation stage, in which a preliminary segmentation of the skull is constructed using a region-growing method. The surface that bounds the pre-segmented skull region offers an automatic 3D initialization of the deformable model. This surface is then propagated (in 3D) in the direction of its normal. This propagation is achieved using level set method, thus permitting changes to occur in the topology of the surface as it evolves, an essential capability for our problem. The speed at which the surface evolves is a function of the estimated partial volume. This provides a sub-voxel accuracy in the resulting segmentation. |
This work is described in a pair of papers (one of
which is written in French! et non, ce n'etait pas moi qui l'a ecrit):
| |
| | |
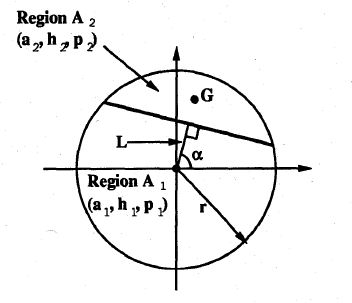
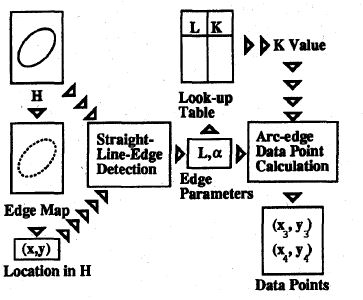
Image Fusion and Subpixel Parameter Estimation for Automated Optical Inspection of Electronic ComponentsJames Reed and Seth Hutchinson | |
|
In this work, we developed an approach to automated optical inspection (AOI) of circular features that combines image fusion with subpixel edge detection and parameter estimation. Several digital images are taken of each part as it moves past a camera, creating an image sequence. These images are fused to produce a high-resolution image of the features to be inspected. Subpixel edge detection is performed on the high-resolution image, producing a set of data points that is used for ellipse parameter estimation. The fitted ellipses are then back-projected into 3-space in order to obtain the sizes of the circular features being inspected, assuming that the depth is known. The method is accurate, efficient, and easily implemented. We obtained experimental results for real intensity images of circular features of varying sizes, and our results demonstrated that their algorithm shows greatest improvement over traditional methods in cases where the feature size is small relative to the resolution of the imaging device. |
| This work is described in James' paper: Back to top | |
| | |
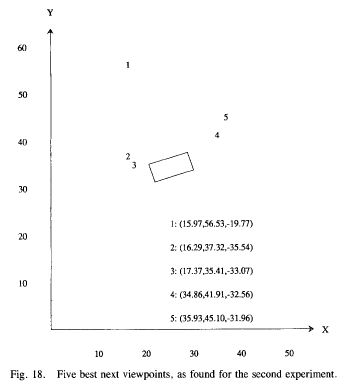
Planning Sensing Strategies in a Robot Work Cell with Multi-Sensor CapabilitiesAvi Kak and Seth Hutchinson | |

|
In this work,
we developed an approach for planning sensing strategies dynamically on the
basis of the system's current best information about the world.
The approach is for the system to propose a sensing operation automatically and then to
determine the maximum ambiguity which might remain in the world description if
that sensing operation were applied.
The system then applies that sensing operation which minimizes this ambiguity.
To do this, the system formulates
object hypotheses and assesses its relative belief in those hypotheses to
predict what features might be observed by a proposed sensing operation.
Furthermore, since the number of sensing operations available to the system can
be arbitrarily large, equivalent sensing operations are grouped together using
a data structure that is based on the aspect graph. In order to measure the
ambiguity in a set of hypotheses, we apply the concept of entropy from
information theory. This allows them to determine the ambiguity in a hypothesis
set in terms of the number of hypotheses and the system's distribution of
belief among those hypotheses.
The figure at the left shows a light-stripe image from a range scan, the segmented image, and the five next best views relative to the object. This work was described in my first real journal paper, a long time ago... |
| Back to top | |
| | |
 |
Seth Hutchinson |
Roboticist |