Visual Servo ControlI first became interested in visual servo control in the late 1980's. In those days, I was at Purdue University, working with Avi Kak in the Purdue Robot Vision Lab. John Feddema, one of the pioneers of visual servo control, was at Purdue at the same time, and it was through John that I first learned about visual servo control. When I joined the University of Illinois in 1990, I began my own research program in visual servo, motivated in large measure by the work that John and others had done in the eighties. Since that time, my group has developed both visual servo control algorithms and planning algorithms for visual servo systems. In addition, I've had the chance to coauthor a couple of tutorials on the topic, first with Greg Hager and Peter Corke, and later with Francois Chaumette. Below, you'll find brief descriptions of the following projects:
| |
| | |
The Tutorialswith Greg Hager, Peter Corke | |
 |
In 1994, Greg Hager, Peter Corke and I organized the first workshop on visual servo control, the IEEE Workshop on Visual Servoing: Achievements, Applications and Open Problems. This workshop was one of the first times that a critical mass of visual servo researchers had been brought together. Soon after this, Greg and I served as guest editors for a special section on visual servo control (the first time an organized collection of visual servo papers had been published together in a journal) in the IEEE Trans. on Robotics and Automation. The issue included the paper A Tutorial on Visual Servo Control (written by Hutchinson, Hager and Corke). Some of the notation is now a bit dated, but the derivations and basic taxonomy of visual servo systems are still relevant. |
with Francois Chaumette | |
 |
A decade later, Francois Chaumette invited me to coauthor a two-part tutorial article for the Robotics and Automation Magazine. In the first article, Visual Servo Control, Part I: Basic Approaches (published in 2006), we described the basic techniques of visual servo control in modern notation. This article included a derivation of the interaction matrix for point features, methods for approximating the interaction matrix, and the basics of stability analysis using Lyapunov methods. In the second article Visual Servo Control, Part II: Advanced Approaches, (published in 2007), we described some of the more advanced methods of current use in visual servo research, including 2 1/2-D, partitioned, and switched visual servo control methods. the articles also consider issues ranging from parameter estimation, optimization, and target tracking. |
|
Back to top | |
| | |
Switched Visual ServoNicholas Gans and Seth Hutchinson | |
 |
For his PhD thesis, my student
Nick Gans
investigated switched visual servo controllers.
Visual servoing methods are commonly classified as image-based or
position-based, depending on whether image features or the camera position
define the signal error in the feedback loop of the control law. Choosing one
method over the other gives asymptotic stability of the chosen error but
surrenders control over the other.
This can lead to system failure if feature
points are lost or the robot moves to the end of its reachable space.
Nick developed hybrid switched-system visual servo methods that use both
image-based and position-based control laws. He proved the stability of a
specific, state-based switching scheme and
and verified performance in simulation and with a real
eye-in-hand system.
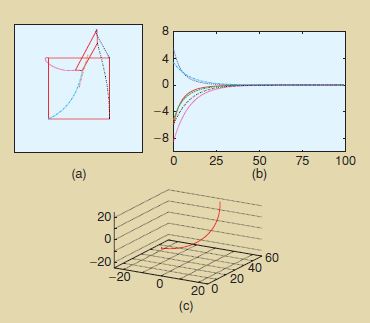
The figure to the left shows the execution of his controller on the famous Chaumette Conundrum (so-named by Peter Corke, I think). For this problem, pure rotation about the optic axis would achieve the goal, but traditional image-based approaches drive the system to the singularity at infinity. Chaumette first described this problem at the Block Island Workshop on The Confluence of Vision and Control in 1996. |
Most of Nick's results are contained in his T-RO paper:
Back to top | |
| | |
Partitioned Visual Servo ControlPeter Corke and Seth Hutchinson | |
 |
Peter Corke (a world famous field roboticist)
visited the University of Illinois around the turn of the century.
During his visit, he and I spent a good deal of time working
through papers written by French people --- the 2.5D visual servo work
of Malis and Chaumette, and the paper of Faugeras and Lustman
on estimating motion from two images of a planar target.
We even delved into the PhD thesis of Chaumette (et oui,
on l'a lu --- meme en francais!!).
At the end of this adventure,
we introduced what I think is the first truly image-based
partitioned visual control system (i.e., all control signals
are derived from quantities that are directly measurable
in the image, with no reconstruction of 3D information about the
scene).
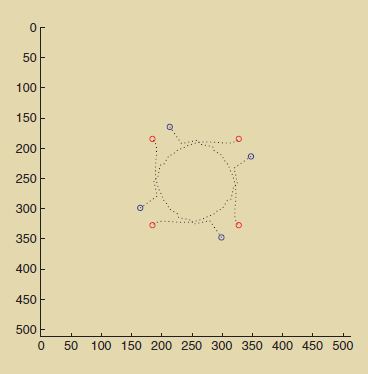
The image at the left shows a typical image feature trajectory of a four-point target during a general visual servo task. |
|
Most of our results can be found in the following paper: Back to top | |
| | |
Visual Compliance - PlanningArmando Fox and Seth Hutchinson | |
 |
In the early nineties, we introduced an approach to exploit
visual constraints in both the planning and execution of robot tasks.
The basic idea was to construct visual constraint surfaces
as the ruled surfaces defined by 3D features
and their projection onto the image plane.
This work was the first to formalize motion planning for
visual servo systems.
Our approach was an extension of earlier work done with preimages,
backprojections and nondirectional backprojections,
all of which had been introduced in the context of
planning for robots with force controllers
(starting with Lozano-Perez, Mason and Taylor,
and then Erdmann and Donald).
We extended these ideas to case of visual constraint surfaces.
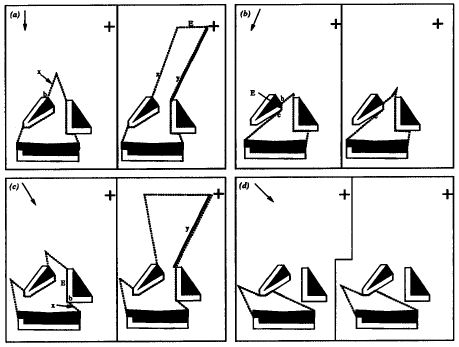
The image to the left shows a few sample slices from the nondirectional backprojection for a simple two-dimensional environment with one-dimensional visual constraint surfaces. |
Visual Compliance - ControlAndres Castano and Seth Hutchinson | 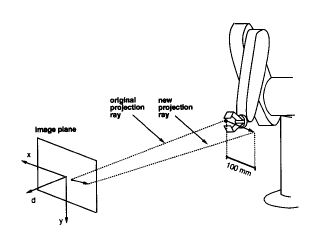 |
Visual compliance is effected by a hybrid vision/position control structure. Specifically, the two degrees of freedom parallel to the image plane of a supervisory camera are controlled using visual feedback, and the remaining degree of freedom (perpendicular to the camera image plane) is controlled using position feedback provided by the robot joint encoders. With visual compliance, the motion of the end effector is constrained so that the tool center of the end effector maintains "contact" with a specified projection ray of the imaging system. This type of constrained motion can be exploited for grasping, parts mating, and assembly. This control architecture was one of the earliest partitioned visual servo control schemes. |
|
The control and planning systems are described in the following papers, both of which were published in the IEEE Trans. on Robotics and Automation.
Back to top | |
| | |
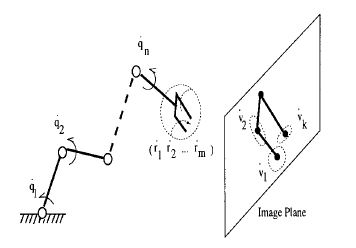
Motion PerceptibilityRajeev Sharma and Seth Hutchinson | |
 |
In the 1990's, Rajeev Sharma
spent some time at the University of Illinois as a Beckman Fellow.
Rajeev and I the introduced the concept of
motion perceptibility,
a quantitative measure of the ability of a computer vision
system to perceive the motion of an object (possibly a robot manipulator)
in its field of view.
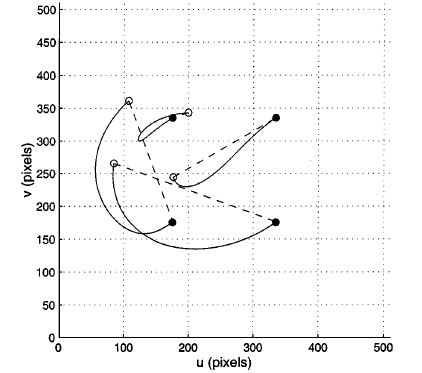
The image to the left illustrates the concept of motion perceptibility. For end-effector velocities with unit norm, the motion perceptibility for three distinct features is illustrated by the ellipses in the image plane. |
|
This work is described in the following paper, which was published
in the IEEE Trans. on Robotics and Automation.
Back to top | |
| | |
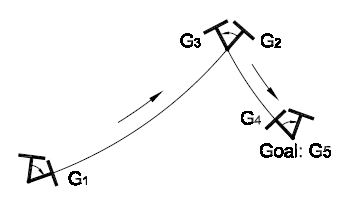
Homography-Based Control for Mobile Robots With Nonholonomic and Field-of-View ConstraintsG. Lopez-Nicolas, N. Gans, S. Bhattacharya, C. Sagues, J. J. Guerrero, and Seth Hutchinson | |
 |
In 2006, Gonzalo Lopez-Nicolas visited my lab in the Beckman Institute.
He met my student Sourabh Bhattacharya,
who was working on the problem of planning optimal paths for
nonholonomic robots with field-of-view constraints
(described in his
T-RO paper),
and my student Nick Gans who was working on switched visual servo systems.
Gonzalo worked to use visual servo methods to implement a controller that
could track the optimal paths.
The result of our collaboration (which also included C. Sagues and J. J. Guerrero) was a visual servo controller that effects optimal paths for a nonholonomic differential drive robot with field-of-view constraints imposed by the vision system. The control scheme relies on the computation of homographies between current and goal images, but unlike previous homography-based methods, it does not use the homography to compute estimates of pose parameters. Instead, the control laws are directly expressed in terms of individual entries in the homography matrix. In particular, we developed individual control laws for the three path classes that define the language of optimal paths: rotations, straight-line segments, and logarithmic spirals. These control laws, as well as the switching conditions that define how to sequence path segments, are defined in terms of the entries of homography matrices. The selection of the corresponding control law requires the homography decomposition before starting the navigation. We provided a controllability and stability analysis for our system along with experimental results. |
| This work is described in the following paper Back to top | |
| | |
 |
Seth Hutchinson |
Roboticist |