Path PlanningPath planning is the quintessential problem in algorithmic robotics. In its most basic form, the problem is to find a collision-free path for a free-flying rigid object moving in an environment populated with stationary obstacles. By increasing the number of degrees of freedom of the robotic system (e.g., by considering articulated kinematic chains or multi-robot systems), or by relaxing constraints on the environment (e.g., allowing obstacles to move), one can construct a broad range of problems that qualify as path planning problems. Our research has considered several variations of the path planning problem, and our contributions include both planning algorithms as well as graph algorithms that support the path planning process. An overview of the main projects is given below.
| | Path Planning for HumanoidsSalvatore Candido, Yong-Tae Kim and Seth Hutchinson |

Path planning for walking robots is both a computationally expensive and
theoretically challenging problem. A typical bipedal robot has a high degree of
actuation, which gives the robot a wide range of motion. Although this is advantageous
for many tasks, because of the complexity of the robot's configuration space
and its stability requirements, it becomes difficult to find a trajectory to
navigate the robot between arbitrary locations. A common strategy to deal with
this complexity is to use a set of motion primitives for a given robot.
Unfortunately, reducing the robot's controls to a discrete set of motion
primitives creates a search problem that is also intractable. We have developed
two main algorithms that deliver heuristics and approximations that allow paths
to be planned quickly while not greatly sacrificing the quality of the
sequences of motion primitives chosen.
| This collaboration with Professor Yong-Tae Kim took place during his visit to my lab in the Beckman Institute.
This work is described in the following papers.
| | | Path Planning for Permutation-Invariant FormationsStephen Kloder and Seth Hutchinson |
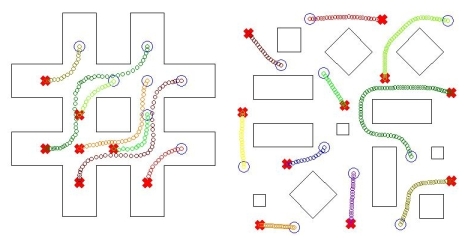
In many multirobot applications, the specific assignment of goal configurations
to robots is less important than the overall behavior of the robot formation.
In such cases, it is convenient to define a permutation-invariant multirobot
formation as a set of robot configurations, without assigning specific
configurations to specific robots. For the case of robots that translate in the
plane, we can represent such a formation by the coefficients of a complex
polynomial whose roots represent the robot configurations. Since these
coefficients are invariant with respect to permutation of the roots of the
polynomial, they provide an effective representation for permutation-invariant
formations. In this work, we extend this idea to build a full representation
of a permutation-invariant formation space. We have
described the properties of the
representation, and shown how it can be used to construct collision-free paths
for permutation-invariant formations
| The figure to the left shows two examples of collision-free paths for permutation-invariant formations.
This work is described in our T-RO paper:
Back to top
| | | Optimal Paths for Landmark-Based NavigationSourabh Bhattacharya and Seth Hutchinson |
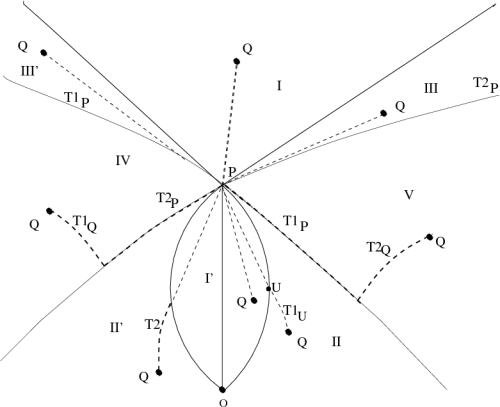
In this work, we considered the problem of planning optimal paths for a
differential-drive robot with limited sensing, that must maintain visibility of
a fixed landmark as it navigates in its environment.
We assume that the robot's vision sensor has a limited field of view (FOV),
and that the
fixed landmark must remain within the FOV throughout the robot's motion.
We first investigated the nature of extremal paths that satisfy the FOV constraint.
These extremal paths saturate the camera pan angle. We then showed that optimal
paths are composed of straight-line segments and sections of these these
extremal paths. We provided a characterization of the shortest paths
for the system by partitioning the plane into a set of disjoint regions, such
that the structure of the optimal path is invariant over the individual regions
| The figure to the left illustrates the partition of the plane that defines regions in which the various types of trajectory are optimal.
This work is described in Sourabh's T-RO paper:
Back to top
| | | Real-Time Path Planning in Changing EnvironmentsPeter Leven and Seth Hutchinson |
In this work,
we
presented a method for generating collision-free paths for robots
operating in changing environments.
Our approach is closely related to probabilistic roadmap approaches.
These planners use preprocessing and query
stages, and are aimed at planning many times in the same environment.
In contrast, our preprocessing stage creates a representation of the configuration
space that can be easily modified in real time to account for changes in the
environment, thus facilitating real-time planning.
As with previous approaches,
we begin by constructing a graph that represents a roadmap in the configuration
space, but we do not construct this graph for a specific workspace.
Instead, we construct the graph for an obstacle-free workspace,
and encode the mapping from
workspace cells to nodes and arcs in the graph.
When the environment changes,
this mapping is used to make the appropriate modifications to the graph, and
plans can be generated by searching the modified graph.
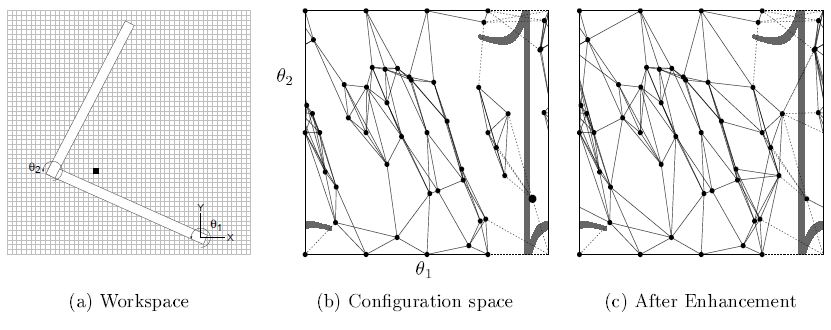
| The figure above shows a simple example. On the left, a two-link planar arm is located in a workspace that contains a single obstacle (the small black square). The middle figure illustrates the mapping of the obstacle from the workspace to the configuration space, superimposed on an existing configuration-space roadmap. The figure on the right shows the roadmap after enhancement.
This work is described in Peter's IJRR paper:
Back to top
| | | Manipulability-Based Sampling for Probabilistic RoadmapsPeter Leven and Seth Hutchinson |
Probabilistic roadmaps (PRMs) are a popular representation used by many current
path planners. Construction of a PRM requires the ability to generate a set of
random samples from the robot's configuration space, and much recent research
has concentrated on new methods to do this.
In this work, we developed a
sampling scheme that is based on the manipulability measure associated with a
robot arm.
Intuitively, manipulability characterizes the arm's freedom of
motion for a given configuration.
Thus, our approach is to densely sample those
regions of the configuration space in which manipulability is low (and
therefore, the robot has less dexterity),
while sampling more sparsely those regions in which the manipulability is high.
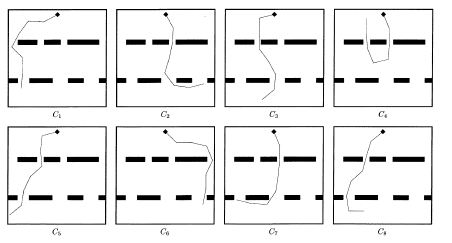
The figure above shows a few typical sample configurations.
|
This work is described in Peter's T-RO paper:
Back to top
| | | Coordination on RoadmapsSteve LaValle and Seth Hutchinson |
This work made two contributions to geometric motion planning for multiple
robots: 1) motion plans are computed that simultaneously optimize an
independent performance measure for each robot; 2) a general spectrum is
defined between decoupled and centralized planning, in which we introduce
coordination along independent roadmaps.
By considering independent performance
measures, we introduced a form of optimality that is consistent with concepts
from multiobjective optimization and game theory literature.
We implemented multiple-robot motion planning algorithms that are derived from
the principle of optimality, for three problem classes along the spectrum
between centralized and decoupled planning: coordination along fixed,
independent paths; coordination along independent roadmaps; and general,
unconstrained motion planning.
|
This work is described in Steve's T-RA paper:
Back to top
| | | Efficient Search and Hierarchical Motion Planning By Dynamically Maintaining Single-Source Shortest Paths TreesMichael Barbehenn and Seth Hutchinson |
Hierarchical approximate cell decomposition is a an approach to the
geometric robot motion planning problem.
In many cases, the search effort
expended at a particular iteration can be greatly reduced by exploiting the
work done during previous iterations. In this work, we described how this
exploitation of past computation can be effected by the use of a dynamically
maintained single-source shortest paths tree.
Our approach was to embed a single-source shortest
paths tree in the connectivity graph of the approximate representation of the
robot configuration space. This shortest paths tree records the most promising
path to each vertex in the connectivity graph from the vertex corresponding to
the robot's initial configuration. At each iteration, some vertex in the
connectivity graph is replaced with a new set of vertices, corresponding to a
more detailed representation of the configuration space. Our dynamic
algorithm is then used to update the single-source shortest paths tree to
reflect these changes to the underlying connectivity graph.
|
This work is described in the following T-RO paper:
Back to top
| | | An Integrated Architecture for Robot Motion Planning and Control in the Presence of Obstacles with Unknown TrajectoriesRobert Spence and Seth Hutchinson
In this work,
we presented an integrated architecture for real-time planning and control of
robot motions, for a robot operating in the presence of moving obstacles whose
trajectories are not known a priori. The architecture comprises three control
loops: an inner loop to linearize the robot dynamics, and two outer loops to
implement the attractive and repulsive forces used by an artificial potential
field motion planning algorithm.
From a control theory perspective, our approach is unique in that the outer
control loops are used to effect both desirable transient response and collision avoidance.
From a motion planning perspective,
our approach is unique in that the dynamic characteristics of both
the robot and the moving obstacles are considered.
|
This work is described in Rob's IEEE SMC paper:
Back to top
| | | |||||||||||||||||||||||||||||||||
 |
Seth Hutchinson |
Roboticist |