Planning Under UncertaintyA robot's knowledge about the state of the world (including the robot itself) derives from two sources: the actions that the robot performs, and the data it obtains using its sensors. The robot's actions, which are typically formalized in a process model, are subject to a variety of uncertainties, both intrinsic (e.g., inaccurate actuation of joints) and extrinsic (e.g., inaccurate models of friction for mobile robots). Sensing, which is typically formalized in an observation model, is also an inaccurate enterprise. Here uncertainties can be due to physical limitations of the sensor (e.g., depth of focus, limited resolution), or to noise in the sensing process. Of course it is possible to ameliorate the effects of uncertainty at run time by designing better control systems or better sensing systems, or even by combining the two (e.g., as with visual servo control), but it is also possible to consider uncertainty during the planning process. With the latter approach, rather than designing algorithms to reduce uncertainty during execution, one designs plans that are robust to uncertainty during plan execution. This general approach is sometimes referred to as planning under uncertainty. Over the years, my group has taken a variety of approaches to this problem. In the earliest work, uncertainty was modeled using bounded sets, and symbolic constraint manipulation techniques were used to propagate uncertainty through the steps in a plan. Later, we investigated Bayesian methods and formalized the concept of a performance preimage, which is essentially the set of configurations from which plan execution is guaranteed to exceed certain performance criteria, even in the presence of uncertainty. In our most recent work, we have adopted the formalism of partially observed Markov decision processes (POMDPs), and focused on efficient algorithms for building approximately optimal policies. An overview of the main projects is given below. | |
| | |
Sampling in the Hyperbelief SpaceJames Davidson, Salvatore Candido and Seth Hutchinson | |
 |
|
|
Typically, the location of a robot is described by a configuration.
If there is uncertainty in the configuration, one can lift the
configuration space into the belief space, which is essentially
the set of possible probability functions for the robot's
position (in this case, a belief is merely an a posteriori
pdf on the robot's configuration).
If a robot system plans into the future, the future beliefs will
depend on future sensor measurements, which cannot be known
at planning time.
To deal with this, we can lift the belief space to the
hyperbelief space, which is merely the set of all possible
pdfs on the belief space.
In the hyperbelief space, policies have deterministic effects
(i.e., for a specific control policy, the transition from
one stage of execution to the next is deterministic).
Thus, in the higher-dimensional hyperbelief space,
one need not (explicitly)
worry about the representation of uncertainty.
Thus, it can be convenient to model
partially observed Markov decision processes (POMDPs)
in the hyperbelief space.
We have developed an anytime algorithm for determining nearly optimal policies for total cost and finite time horizon POMDPs using a sampling-based approach. The technique, sampling hyperbelief optimization technique (SHOT), builds a roadmap in the hyperbelief space. The method exploits the notion that small changes in a policy have little impact on the quality of the solution except at a small set of critical points. The result is a technique to represent POMDPs independent of the initial conditions and the particular cost function, so that the initial conditions and the cost function may vary without having to re-perform the majority of the computational analysis. | |
| The basic ideas, along with some results, are given in the following WAFR paper: Back to top | |
| | |
Minimum Uncertainty Robot Path Planning using a POMDP ApproachSal Candido, James Davidson and Seth Hutchinson | |
| We have developed a minimum uncertainty planning technique for mobile robots localizing with beacons. We model the system as a partially-observable Markov decision process and use a sampling-based method in the belief space (the space of posterior probability density functions over the state space) to find a belief-feedback policy. This approach allows us to analyze the evolution of the belief more accurately, which can result in improved policies when common approximations do not model the true behavior of the system. Our experimental evaluations demonstrate that our method performs comparatively, and in certain cases better, than current methods in the literature. | |
|
Preliminary results are given in a forthcoming IROS paper (not yet
available).
Back to top | |
| | |
Exploiting Domain Knowledge when Learning Policies for POMDPsSal Candido, James Davidson and Seth Hutchinson | |
|
We have developed a planning algorithm that allows user-supplied domain knowledge to
be exploited in the synthesis of information feedback policies for systems
modeled as partially observable Markov decision processes (POMDPs). POMDP
models, which are increasingly popular in the robotics literature, permit a
planner to consider future uncertainty in both the application of actions and
sensing of observations. With our approach, domain experts can inject
specialized knowledge into the planning process by providing a set of local
policies that are used as primitives by the planner. If the local policies are
chosen appropriately, the planner can evaluate further into the future, even
for large problems, which can lead to better overall policies at decreased
computational cost. We use a structured approach to encode the provided domain
knowledge into the value function approximation.
We have applied our approach to a multi-robot fire fighting problem, in which a team of robots cooperates to extinguish a spreading fire, modeled as a stochastic process. The state space for this problem is significantly larger than is typical in the POMDP literature, and the geometry of the problem allows for the application of an intuitive set of local policies, thus demonstrating the effectiveness of our approach. | |
| The early results for this project are given in an ICRA paper: Back to top | |
| | |
An Objective-Based Framework for Motion Planning Under Sensing and Control UncertaintiesSteve LaValle and Seth Hutchinson | |
 |
|
|
This work was initially inspired by the preimage planning methods
of Lozano-Perez, Mason and Taylor, Erdmann, and Donald.
Preimage planning involves worst-case analysis.
Our method presented a general framework for determining feedback strategies
by blending ideas from stochastic optimal control and dynamic game theory with
traditional preimage planning concepts.
This generalizes classical preimages to
performance preimages and preimage planning for designing motion strategies
with information feedback.
For a given problem, one can define a performance
criterion that evaluates any executed trajectory of the robot.
Our method selects a motion strategy that optimizes this criterion
under either nondeterministic uncertainty (resulting in worst-case analysis) or
probabilistic uncertainty (resulting in expected-case analysis).
We implemented the method using dynamic programming
algorithms that numerically compute performance preimages and optimal strategies.
The image above shows, from left to right, computed optimal strategies, performance preimages and several sample paths. | |
| The primary results for this project are given in Steve's IJRR paper: Back to top | |
| | |
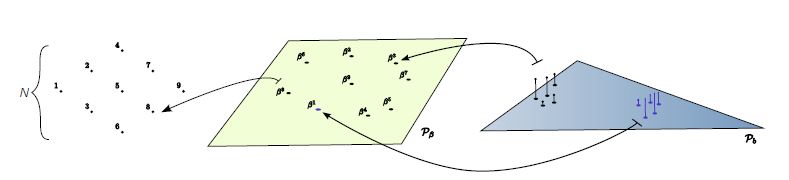
Optimizing Robot Motion Strategies for Assembly with Stochastic Models of the Assembly ProcessRajeev Sharma, Steve LaValle and Seth Hutchinson | |
 |
Gross-motion planning for assembly is commonly considered as a distinct,
isolated step between task sequencing/scheduling and fine-motion planning.
In this work, we formulate a problem of delivering parts for assembly in
a manner that integrates it with both the manufacturing process and the fine
motions involved in the final assembly stages. One distinct characteristic of
gross-motion planning for assembly is the prevalence of uncertainty involving
time (in parts arrival, in request arrival, etc.).
Our approach uses
stochastic representation of the assembly process, and
produces a state-feedback controller that optimizes the expected
time that parts wait to be delivered.
This leads to increased performance and a greater likelihood of stability in a
manufacturing process.
We demonstrated the method on
six specific instances of the general framework,
each of which were solved to yield optimal motion strategies for different robots
operating under different assembly situations.
The image to the left shows a stylized representation of an assembly process in which parts arrive with random arrival times from multiple sources, and must be assembled in the robotic work cell. |
| The main results are given in the following paper: Back to top | |
| | |
SPAR: A Planner that Satisfies Operational and Geometric Goals in Uncertain EnvironmentsAvi Kak and Seth Hutchinson | |
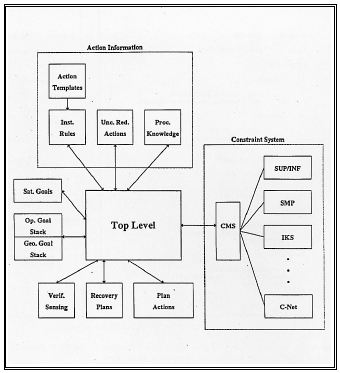 |
Spar (simultaneous planner for assembly robots) is a planner that reasons about high-level operational goals, geometric goals, and uncertainty-reduction goals to create task plans for an assembly robot. These plans contain manipulations to achieve the assembly goals and sensory operations to cope with uncertainties in the robot's environment. High-level goals (which we refer to as operational goals) are satisfied by adding operations to the plan using a nonlinear, constraint-posting method. Geometric goals are satisfied by placing constraints on the execution of these operations. If the geometric configuration of the world prevents this, Spar adds new operations to the plan along with the necessary set of constraints on the execution of these operations. When the uncertainty in the world description exceeds that specified by the uncertainty-reduction goals, Spar introduces either sensing operations or manipulations to reduce this uncertainty to acceptable levels. If Spar cannot find a way to sufficiently reduce uncertainties, it augments the plan with sensing operations to be used to verify the execution of the action and, when possible, posts possible error-recovery plans. |
| The main ideas are given in the following paper: Back to top | |
| | |
 |
Seth Hutchinson |
Roboticist |